Mathématiques
Aire maximale d’un triangle dans un cercle
Niveau 6e - 5e ; Géométrie dynamique
mardi, 20 décembre 2011
http://maths.ac-amiens.fr/038-aire-maximale-d-un-triangle-dans-un-cercle.html
Facile
Manipulation de l’ordinateur
En groupe
Présentation de l’activité
Sur un cercle de centre A, où placer les points B et C pour que l’aire du triangle ABC soit la plus grande possible ?
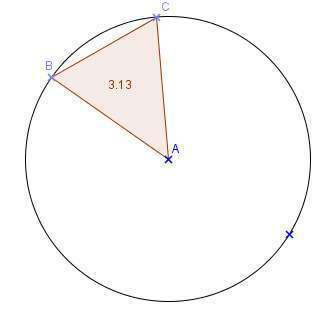
Public / Niveau
- Sixième (avec une condition qui limite l’angle
 )
) - Cinquième (sans condition sur l’angle
 )
)
Objectifs
- Résolution d’un problème : recherche d’un maximum
- Réinvestissement du calcul de l’aire d’un triangle rectangle
Durée
- 1h pour la recherche en salle informatique
- 30 min pour aborder l’explication
Notions réinvesties
- Programme de construction
- Mesure d’un angle
- Calcul de l’aire d’un triangle rectangle
Déroulement de l’activité
- Appropriation du sujet
- Sur table, les élèves découvrent le sujet :
- Lecture collective du programme de construction ;
- Explication des mots ou des notations qui peuvent paraitre difficiles (rayon quelconque ; notation de l’angle ; angle inférieur à 90°) ;
- Réalisation d’une figure respectant le programme de construction (la condition n°3 sur l’angle
 peut induire certains élèves en erreur ; si c’est le cas, demander si cet angle doit être aigu ou obtus ;
peut induire certains élèves en erreur ; si c’est le cas, demander si cet angle doit être aigu ou obtus ; - Synthèse collective sur les diverses constructions.
- Présentation succincte au vidéoprojecteur de GeoGebra
- Recherche TICE : Sur ordinateur, 1 ou 2 élèves par poste. Les élèves n’ont jamais utilisé GeoGebra mais connaissent un autre LGD : Déclic
- Réalisation de la figure et manipulation du point C ;
- Conjecture d’une solution au problème posé ;
- Reproduction d’une configuration « solution » et d’une autre qui n’est pas « solution ». (On pourra faire apparaitre la mesure de l’angle
 si l’élève a du mal à formuler la conjecture)
si l’élève a du mal à formuler la conjecture)
--- fin de la première heure ---
- Recherche d’une preuve
- Retour en classe entière :
- Rappel au vidéoprojecteur du problème ;
- Tracé au tableau des deux figures pour comparer les aires des triangles ABC. (Il est préférable de fixer une mesure au rayon du cercle pour permettre un calcul d’aire) ;
- Le calcul de l’aire du triangle rectangle ne pose pas de problème mais celle du triangle quelconque demande réflexion. L’idée de le décomposer en triangles rectangles apparait chez certains élèves. On termine le calcul ;
- Aucune exigence de rédaction n’est demandée, la réflexion est orale et collective. L’enseignant guide simplement le débat en distribuant la parole.
Apport des TICE
Passage d’une géométrie des mesures à une géométrie des propriétés.
L’utilisation d’un logiciel de géométrie dynamique permet de « tester toutes les possibilités » pour arriver à une conjecture, chose qui peut être encore inaccessible à certains élèves de sixième.
Prolongements possibles
Pour des élèves de 5ème, on peut enlever la condition sur l’angle ![]() la solution est d’autant plus riche car le maximum n’est alors plus une condition au bord.
la solution est d’autant plus riche car le maximum n’est alors plus une condition au bord.
Personne à contacter pour cette activité : Sylvain ANSART
En visitant la page http://maths.ac-amiens.fr/038-aire-maximale-d-un-triangle-dans-un-cercle.html, vous pourrez télécharger ces documents :
- Figure GeoGebra, (Fichier GeoGebra - 3.3 kio)
- Document donné aux élèves, (Word - 23.5 kio)
- Document donné aux élèves, (PDF - 113.4 kio)