Mathématiques

Le cahier de référence mutualisé

dimanche, 29 janvier 2012

http://maths.ac-amiens.fr/094-le-cahier-de-reference-mutualise.html

Production académique pour les travaux académiques mutualisés 2010-2011, réalisée par E. Agnel, A. Baraquin, V. Maille, G. Miannay et F. Prédinas.

Le point de départ

L’idée de cette réflexion est née lors de la synthèse des travaux académiques mutualisés de 2009 – 2010.
Lors des retours par les différentes académies, nous avions eu différents exemples sur l’utilisation d’un cahier de texte enrichi pour l’élève. Les ressources étaient très intéressantes, mais, le temps nécessaire à la création et à la mise en ligne des ressources ne permettent pas en toute objectivité de réaliser cela durant toute l’année. D’autant que pour beaucoup de cahiers de textes, le travail est perdu en fin d’année.

Évidemment s’il s’agit de cahiers de textes, cela est compréhensible, car les années se suivent mais ne se ressemblent pas... quoique d’une année sur l’autre, certaines choses changent (méthode d’approche, ordre des notions, ...) mais d’autres restent (le théorème de Pythagore ou le calcul des coordonnées du milieu d’un segment).

Une autre problématique se posait, nous sommes plusieurs à essayer de « spiraler » notre enseignement, et la question des traces de cours pose un réel problème de gestion.

Nous avons donc réfléchi à un cahier de référence interactif pour nos élèves qu’ils pourront utiliser afin :

• De préparer un devoir,
• De corriger un devoir,
• De travailler sur une activité en utilisant la plateforme comme accompagnement...

Il ne s’agit donc plus d’un cahier de texte, ni d’un manuel numérique modulable (nous n’y trouverons pas d’activités d’introduction d’un chapitre par exemple) mais de fiches de cours facilement manipulables par l’enseignant pour permettre aux élèves de conserver une trace d’une progression spiralée tout au long de l’année. La gestion d’un classeur posant souvent encore problème.

Le cahier des charges

Proposer un cours modulable constitué de briques (définition, figure, propriété, ...) et d’autres éléments (liens, titres, texte, ...). C’est la principale différence avec un cahier de référence classique : ici on n’a pas un grimoire qui peut donner l’impression de recéler toutes les méthodes pour résoudre un problème de mathématiques, mais ce système offre à l’enseignant la possibilité de placer les blocs qu’il souhaite au fur et à mesure.

Il faut donc donner au professeur la possibilité d’organiser sur une fiche les briques comme il l’entend (comme sur une plateforme moodle : déplacer, montrer/cacher pour faire le travail à l’avance).

Prenons l’exemple de la notion d’intervalle. Au vu des nouveaux programmes, l’enseignant n’est pas sensé faire un chapitre synthétique sur cette notion ( I - Intervalles bornés, II - Intervalles non bornés, III - Réunions et Intersections, ...) mais il lui faudra être progressif dans les apprentissages. Selon la progression de l’enseignant, les élèves verront peut être :

• Les intervalles fermés bornés lors de la représentation des fonctions
• Puis plus tard, les intervalles de type ]a ; +∞[, lors de la résolution d’inéquations du premier degré
• Ensuite les réunions avec celles du second degré
• Enfin, ceux du type ]a ;b] avec les inéquations quotient.

Jusqu’à présent un travail avec un classeur et des fiches était souvent réalisé, mais cela entrainait des difficultés de repérage pour les élèves.

Permettre aux professeurs de :

• Créer une brique de toutes pièces,
• Prendre une brique dans la banque :
  • telle quelle,
  • de la modifier.
• Prendre une brique d’un autre collègue qui a décidé de la partager

La banque a pour but de proposer à l’enseignant des briques « certifiées » résultant d’échanges avec le groupe de travail. Mais il paraît aussi important de donner la possibilité à tous de publier et partager leurs briques pour permettre la mutualisation au sein d’un établissement par exemple sans avoir à passer par la « certification ».

On peut donc prendre des briques certifiées et les agréger ensuite dans une fiche !

Côté élève : un moteur de recherche permet de trouver les fiches par mot clef sur le contenu.

Les briques

Une fiche est donc constituée de briques et d’autres éléments propres à la fiche (texte, titre, liens, ...)

Il existe différents types de briques à placer dans une fiche :

• Définition : Contient un texte de définition
• Exemple : Contient un énoncé d’exemple et éventuellement une correction s’il s’agit d’un exercice d’illustration. Par défaut la solution est masquée, l’élève peut choisir de la rendre visible.
• Propriété : Ces briques contiennent un énoncé et lorsque cela est possible et pertinent, une démonstration. La preuve est cachée en première lecture, mais cela permet aux plus curieux d’aller les consulter.
• Méthode : Elle contient des méthodes ou des conseils mathématiques (simplifier une racine, résoudre une équation, ....)
• Figure : Elle contient une figure dynamique (GeoGebra) et une figure alternative fixe ( LaTeX) pour permettre une impression en PDF.

Exemple de création d’une nouvelle brique (cliquer sur les imagettes) :

• Depuis le menu principal, on choisit de voir les briques existantes

• On choisit créer une nouvelle brique

• On renseigne les champs

• Un éditeur LaTeX est disponible.

• On peut alors choisir de partager sa brique avec la communauté

• La brique est compilée (la mise en forme est gérée par le site)

L’enseignant peut se concentrer sur le contenu mathématique de la fiche, puisque la mise en page est gérée par la plateforme. Cela permet aussi une certaine harmonie sur les pages et une meilleure visibilité pour l’élève.

Les fiches

Hormis les briques que l’on peut insérer, certains objets sont propres à la fiche :

• Titre, sections et sous-sections
• Texte
• Liens vers exercices extérieurs
• Liens vers des exercices interactifs Math O’ Lycée
• Liens vers des exercices papier Math O’ Lycée

La navigation sur la fiche doit être aisée :

• Moteur de recherche sur la fiche
• Afficher le sommaire pour se rendre directement à un paragraphe
• Afficher la liste des fiches
• Imprimer en PDF
• Zoom

Pour créer sa propre fiche,

• On peut donc créer une fiche à partir d’une fiche vide (cliquer sur les imagettes) :
  • Entrer dans le menu FICHE depuis la page principale.
    

    

  • Vous obtenez alors une fiche vierge, précisez son titre.
    

    

  • Vous pouvez insérer différents types de briques (ici des propriétés)
    

    

  • Un moteur de recherche permet de filtrer les briques par mot clé ou par auteurs.
    

    

  • Les briques s’insèrent, il reste à préciser la classe et à la publier
    

    

  • Différentes options permettent de finaliser la mise en page et de modifier les briques en direct
    

    

• On peut partir à d’une fiche existante.
  Un certain nombre de fiches existant déjà. Quelques exemples de fiches :
  • Opérations sur les vecteurs
  • Vecteurs et coordonnées
  • Vecteurs et translation

L’enseignant peut les copier sur son compte d’un simple clic et pourra alors les utiliser telles quelles ou les modifier s’il le souhaite (cliquer sur les imagettes).

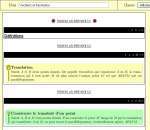
• L’enseignant part d’une fiche de démonstration

• Il peut alors la copier

• Il suffit alors de copier la brique

• Vous pouvez alors la modifier

• Vous avez à présent les droits de modification

• Votre brique est compilée.

• Et votre fiche est actualisée.

La mise en œuvre

De nombreux collègues du groupe de travail sur les TraAM travaillent aussi dans le groupe de Math O’ Lycée, nous avons décidé d’inclure ce nouvel outil sur l’espace Math O’ Lycée.

Pour voir en tant qu’élève, connectez-vous au site : http://mol.ac-amiens.fr/ avec le login 2010.traam et le mot de passe 2010.

Avec nos multiples occupations, nous n’avons eu le temps cette année « que » de réfléchir et de programmer l’outil.

À noter que l’intérêt de ce système réside dans le fait que les fiches peuvent ou non suivre la progression du cours. Ainsi la progression sur l’année peut être spiralée, tout en proposant des fiches « structurées » aux élèves.
Inversement, on peut dispenser un cours très structuré et proposer des fiches transversales de bilan... tout est possible. Selon la demande, d’autres types de briques pourraient voir le jour (Vidéo, animation Instrumenpoche, ...)

À présent l’outil existe, libre à chaque enseignant de l’utiliser ou non, de l’enrichir ou non... Bref, de le faire vivre ou non...