Mathématiques
Transformation complexe
Niveau Terminale S ; Géométrie dynamique
mercredi, 15 février 2012
http://maths.ac-amiens.fr/112-transformation-complexe.html
Facile
Manipulation de l’ordinateur
En groupe
Présentation de l’activité
Étude dans le plan complexe ramené à un repère orthonormé de la transformation complexe qui à un point M d’affixe z, associe le point M’ d’affixe z’ vérifiant : ![]()
Public / Niveau
Terminale S (non spécialité)
Durée
1 h 30
Objectifs
- Étude d’une transformation complexe.
- Utiliser un logiciel de géométrie dynamique pour conjecturer les propriétés
- Travail sur les nombres complexes et la géométrie :
- Distances et modules
- Angles et arguments
Ce qui a été fait avant
Cours sur les nombres complexes et la géométrie
Déroulement de l’activité
L’énoncé est donné aux élèves avec comme consigne d’ouvrir la page internet : "Lancer GeoGebra Complexes" HTML qui se trouve sur le lecteur de la classe.
|
|
Chaque question se déroule en 2 étapes :
- Conjecturer à l’aide du logiciel,
- Démontrer au fur et à mesure sur une feuille.
Un exemple d’étude d’une telle transformation avait déjà été étudié en classe à l’aide du TBI ce qui a permis une certaine imprégnation côté élève.
Fichiers utiles
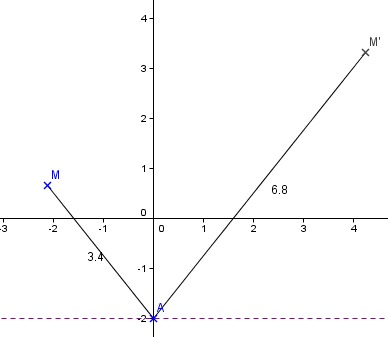
Un exemple de figure réalisée par un élève :
|
|
Évaluation
La partie TICE (Production de la figure) n’a pas été évaluée, seule la copie contenant les conjecture et les preuves a été ramassée.
Apport des TICE
Le fait de pouvoir visualiser la transformation permet à l’élève d’émettre des conjectures. Une fois les conjectures effectuées, il doit alors prendre l’initiative des calculs qui lui permettront d’arriver à la preuve. L’engagement n’est pas le même que dans le sujet d’origine :

Prolongements possibles
Démontrer que seules les droites d’équations x=0 et y=-2 sont en effet globalement invariantes.
Personne à contacter pour cette activité : Vincent MAILLE
En visitant la page http://maths.ac-amiens.fr/112-transformation-complexe.html, vous pourrez télécharger ces documents :
- Lancer_GeoGebra_Complexes.html, (HTML - 2 kio)