Mathématiques

Centre du cercle circonscrit

Niveau 2nde ; Géométrie dynamique - Calcul formel

mercredi, 15 février 2012

http://maths.ac-amiens.fr/114-centre-du-cercle-circonscrit.html

Facile

Manipulation de l’ordinateur

En groupe

Présentation de l’activité

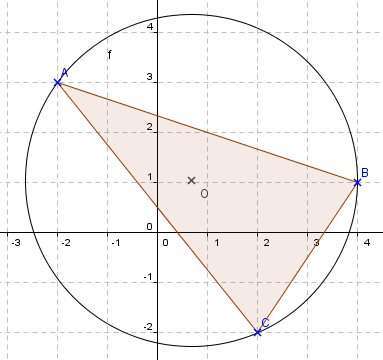
Dans un repère orthonormé, on considère les points A(-2 ;3), B(4 ;1) et C(2 ;-2).
Quelles sont les coordonnées du centre du cercle circonscrit à ABC ?

Public / Niveau

Seconde

Durée

Une heure

Objectifs

• Résoudre un problème de mathématique.
• Se rendre compte que le logiciel de géométrie dynamique ne donne pas les valeurs exactes
• Travail sur la géométrie analytique :
  • Calculs de longueurs
  • Redonner du sens aux équations de droites

Ce qui a été fait avant

• Formules de calculs de distances et de milieux dans un repère
• Équations de droites

Déroulement de l’activité

Les étapes attendues a priori sont :

• Faire une figure (Sur papier ou sur ordinateur).
• Lire une valeur approchée des coordonnées
• Traduire l’énoncé en terme de contraintes mathématiques
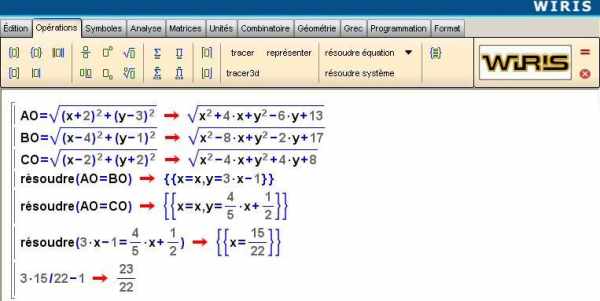
• Les élèves ont donné une expression de la longueur OA en fonction des coordonnées (x ; y) du point O cherché. Idem pour OB et OC (où OA² , OB² et OC² selon les cas)
• Trouver à partir des égalités OA = OB, OB = OC, OC = OA des conditions sur x et y et essayer d’exprimer effectivement x et y.
  Ici, le logiciel de calcul formel permet :
  • De gérer l’hétérogénéité de la classe,
  • De retravailler sur les équations de droites.
• Retour sur GeoGebra :
  • Certains élèves ont tapé l’équation $y=\frac4x5+\frac12 et vu que c’était la médiatrice,
  • D’autres ont tracé la médiatrice et lu l’équation.

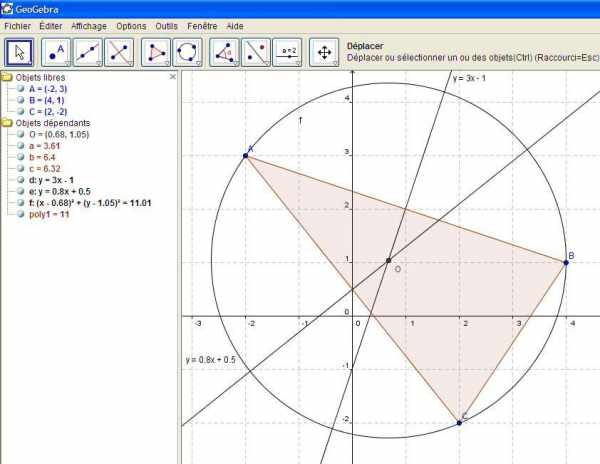
• Selon, les possibilités des élèves, chacun s’est attelé à une étape de la preuve.

Évaluation

J’ai fait une fiche de synthèse pour prendre des notes pendant l’activité et j’ai donné les critères aux élèves.

Évaluation des élèves format PDF - 21.7 kio

Évaluation des élèves format Excel - 21 kio

Apport des TICE

• Le logiciel de Géométrie dynamique n’apporte pas grand chose de plus qu’une figure papier, si ce n’est la précision.
• Le fait d’avoir un ordinateur à portée de main à permis aux élèves les plus faibles, d’aller sur internet retrouver les définitions du centre du cercle circonscrit, médiatrices,...
• Le calcul formel permet à tous d’avancer (voir partie déroulement).

Prolongements possibles

Calcul des coordonnées du centre de gravité.

Personne à contacter pour cette activité : Vincent MAILLE