Mathématiques
Optimisation de l’aire d’un rectangle
Niveau 2nde - 1ère ; Géométrie dynamique
vendredi, 2 mars 2012
http://maths.ac-amiens.fr/178-optimisation-de-l-aire-d-un-rectangle.html
Facile
Manipulation de l’ordinateur
En groupe
Présentation de l’activité
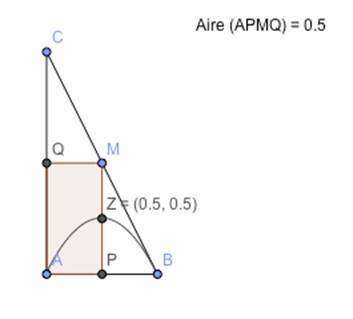
Q appartient à [AC], P appartient à [AB] et M appartient à [BC] tel que APMQ soit un rectangle.
Comment choisir M pour que l’aire du rectangle APMQ soit maximale ?
Public / Niveau
- Première S (utilisation du second degré)
- Possible aussi en Seconde (avec questions pour le second degré)
Durée
1 heure en demie classe : chaque élève dispose d’un ordinateur.
Objectifs
- Première étape : construction de la figure.
- Deuxième étape : conjecturer la position du point M.
- Troisième étape : démontrer le résultat conjecturé.
Ce qui a été fait avant
Cours sur le second degré.
Déroulement de l’activité
- Élèves : utilisation de GeoGebra pour construire la figure.
- Des élèves pensent au milieu P de [AB].
- Avec « polygone », on crée un polygone (ici un rectangle) dont l’aire s’affiche, il suffit de modifier la position de M et émettre la conjecture.
- Professeur :
- Utilisation d’un repère d’origine A et de
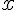 pour préciser la position de P.
pour préciser la position de P. - Utilisation du vidéo-projecteur : figure avec A(0 ;0), B(1 ;0) et C(0 ;2) puis ajout de la “trace activée” de Z(x ;Aire(x) ) qui permet d’appuyer la conjecture des élèves.
Possibilité d’exploiter la courbe obtenue avec la trace.
- Utilisation d’un repère d’origine A et de
Pour la preuve
- Équation de la droite (BC).
- Aire en fonction de x.
- Second degré et variations du trinôme.
Apport des TICE
Créer un figure dynamique permettant de conjecturer le résultat attendu.
Personne à contacter pour cette activité : Guillaume MIANNAY
En visitant la page http://maths.ac-amiens.fr/178-optimisation-de-l-aire-d-un-rectangle.html, vous pourrez télécharger ces documents :
- Fichier GeoGebra, (Fichier GeoGebra - 1.5 kio)