Mathématiques

Espace et équations

http://maths.ac-amiens.fr/197-espace-et-equations.html

Facile

Utilisation d’un vidéo-projecteur

En classe entière

Présentation de l’activité

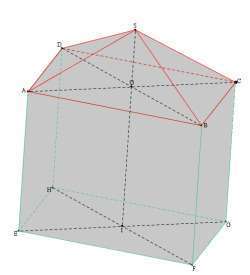
Sur la figure ci-dessous, le pavé de dimensions 10 sur 6 et de hauteur variant entre 0 et 12 est surmonté d’une pyramide à base rectangulaire, la hauteur totale est de 12.

• Pour quelle valeur de CG le volume de la pyramide est-il égal à celui du pavé ?
• Pour quelle valeur de CG le volume de la pyramide est-il égal au double celui du pavé ?

Public / Niveau

Quatrième

Objectifs

• Ré-investir le calcul de volume.
• Justifier la nécessité de résoudre des équations.

Ce qui a été fait avant

Calcul de volumes de pyramides.

Déroulement de l’activité

• Cette figure Geospace a été utilisée en vidéoprojection en classe entière en déplaçant le point C pour faire comprendre la situation : le pavé de dimensions 10 sur 6 et de hauteur variant entre 0 et 12 est surmonté d’une pyramide à base rectangulaire.
• Les élèves sont à ce moment dans la fin du chapitre dans lequel ils ont appris à calculer les volumes de pyramide mais n’ont pas vu le calcul littéral et encore moins les équations.
• Une question est posée en groupe de deux à quatre élèves avec calculatrice autorisée : Pour quelle valeur de CG le volume de la pyramide est-il égal à celui du pavé ?
• Lorsqu’un groupe a trouvé, la deuxième question tombe alors pour ce groupe : Pour quelle valeur de CG le volume de la pyramide est-il égal au double celui du pavé ?" ou une variante « un centimètre cube de plus (ou de moins) que le volume du pavé », par exemple.
• Différentes stratégies sont employées mais si la première question ne résiste pas longtemps, la deuxième, en revanche, en l’absence de technique "experte" faisant appel au calcul littéral donne dans le meilleur des cas une valeur approchée obtenue par essais successifs.
  Les élèves viennent proposer leur valeur qui est essayée... et invalidée grâce à la figure du fichier Geospace ou GeoGebra.
• La séance se conclut par un échec général sur la deuxième question, du moins pour la valeur exacte.
  Ainsi l’introduction du calcul littéral et surtout des équations dont la méthode est toujours, à juste titre, perçue comme "lourde" par les élèves, est justifiée puisque nous (le groupe classe) n’avons pas réussi à trouver de réponse satisfaisante. Cela évite l’écueil du « M’sieur, moi j’ai trouvé sans utiliser TOUT ça » lorsqu’on aborde les équations avec un problème pas assez corsé pour résister au petit futé de service et qui a tôt fait de rendre l’étude du chapitre "équation" très discutable aux yeux des élèves !

Fichiers utiles

Remarque

Les équations obtenues sont du premier degré ().
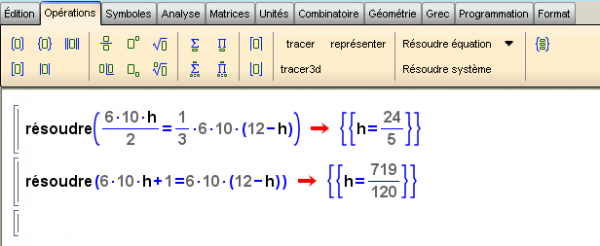
Pour ne pas rester sur un "échec", on peut aller jusqu’à l’écriture de l’équation, que l’on demande alors de résoudre par un logiciel de calcul formel, comme Wiris.

Apport des TICE

• La figure dynamique aide à l’appropriation de la situation et développe la vision dans l’espace.
• La figure dynamique et ses fonctionnalités (affichage des volumes et des longueurs) fait comprendre que le problème a une solution.
• Vérifier ses calculs.
• Voir les limites de la figure dynamique pour motiver la résolution d’équations.

Personne à contacter pour cette activité : Olivier MIRVILLE