Mathématiques

Cubes

Niveau 6e - 5e ; Tableur

mercredi, 21 mars 2012

http://maths.ac-amiens.fr/209-cubes.html

Facile

Utilisation d’un vidéo-projecteur - Manipulation de l’ordinateur

En classe entière - En groupe

Présentation de l’activité

Activité de recherche :
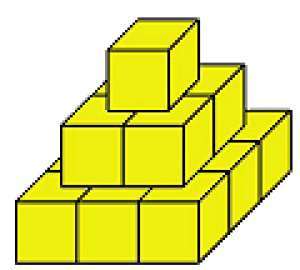
Cette pyramide de 3 étages est composée de 14 cubes.

De combien de cubes une telle pyramide de 10 étages est-elle composée ?
Je dispose de 3000 cubes. Combien d’étages au maximum pourrai-je obtenir ? Combien de cubes me restera-t-il ?

Public / Niveau

Expérimentée en sixième – possible en cinquième.

Pré-requis / Notions investies

Nombres entiers.
Pour l’activité initiale : carrés des nombres entiers.
Pour les activités de réinvestissement : somme, différence.

Ce qui a été fait avant

La formule d’aire du rectangle puis du carré.
La connaissance des carrés des premiers nombres entiers (diagonale de la table de Pythagore).

Déroulement de l’activité

1^er temps : appropriation collective de la situation - manipulation (15 minutes)
- Présentation de la pyramide de 3 étages – dénombrement du nombre de cubes – démontage et remontage.
- Recherche du nombre de cubes permettant de construire une pyramide 2 fois plus haute (6 étages) : c’est l’occasion au passage d’expliciter une situation de non-proportionnalité (réponse immédiate de la quasi-totalité des élèves : 28 cubes) – construction effective de cette nouvelle pyramide.
2^ème temps : recherche individuelle de la première question du problème (10 minutes)
- Recherche individuelle du nombre de cubes de la pyramide à 10 étages (travail sur feuille relevé).
3^ème temps (lors d’une autre séance) : présentation sous la forme d’un tableau de la recherche (apport de l’enseignant)

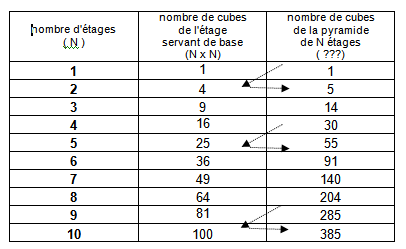
Prolongement du problème en proposant la seconde question : « Je dispose de 3000 cubes. Combien d’étages au maximum pourrai-je obtenir ? Combien de cubes me restera-t-il ? ».
C’est l’occasion de mettre en avant des outils plus performants comme le tableur présentable sans difficulté à la classe si on dispose d’un vidéo-projecteur.

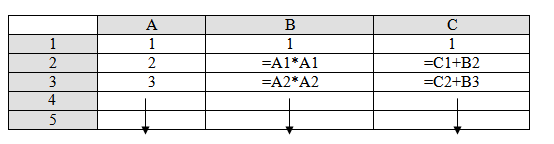
Après duplication de la ligne (A3-B3-C3) vers le bas, on peut faire décrire ce qui se passe dans la colonne A ; dans la colonne B et dans la colonne C.
On peut bien sûr trouver la solution au problème.

4^ème temps : réinvestissement (à étaler dans le temps et à varier dans la forme : séance collective en classe, recherche individuelle en salle de communication, travail personnel)
Proposition de différentes situations se prêtant à ce type de traitement en s’appuyant systématiquement sur un support permettant d’expliciter les formules de calculs comme :

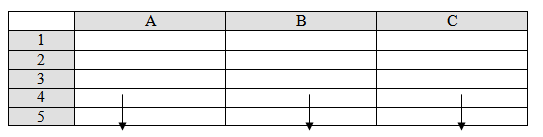
Quelques exemples de situations format PDF - 13.4 kio

Quelques exemples de situations format Word - 29 kio

Apport des TICE

La rapidité du tableur pour accéder, par itération des formules d’une ligne à l’autre, est un atout non négligeable.
Cela relève de la « magie » pour les jeunes élèves. Il faut toutefois prendre le temps de vérifier la validité des formules d’une ligne à l’autre et de leur utilisation convenable par le logiciel.
Comme pour les logiciels de géométrie dynamique pour lequel le travail sur papier et aux outils est complémentaire et nécessaire, la réalisation et la complétion de tableaux sur papier au préalable est nécessaire.

De telles pratiques peuvent amener les élèves à proposer l’utilisation du tableur pour vérifier l’unicité d’une solution à un problème de recherche résolu par essais successifs.
Ainsi, après la résolution par essais successifs d’un problème de recherche à deux équations et deux inconnues à valeurs dans N lors d’une séance d’anglais précédent le cours de mathématiques (épreuve 1 du rallye 2007 « mathématiques sans frontières » de l’académie de Strasbourg), quelques élèves de sixième ont voulu s’assurer que la solution qu’ils avaient obtenu était bien la seule.
Ils ont proposé d’envisager tous les cas possibles. Ici, le nombre de cas à envisager étant réduit, la recherche pouvait être envisager sur papier en fixant une des variables et en la faisant varier de 1 en 1.
Les élèves ont alors reconnu dans cette méthode une procédure gérable par le tableur et ont souhaité l’expliciter. La disponibilité du vidéo-projecteur dans la classe ce jour-là à permis de satisfaire cette sollicitation.

Prolongements possibles

Suivant la situation de récurrence, les élèves ont la possibilité d’émettre des conjectures sur le lien entre la première colonne (nombre d’étages N) et la 3ème colonne sur laquelle la prise d’information aura lieu pour obtenir la solution au problème posé.
Il ne faudra pas rater cette opportunité si elle se présente et suivant le niveau de la classe, des démonstrations peuvent être envisagées.

Ainsi, pour la première situation de réinvestissement (l’escalier), ils pourront envisager l’hypothèse que la somme des N premiers nombres impairs est égale au carré de N.
Une démonstration telle que celle ci-dessous est certainement envisageable en cinquième :

donc $2S_n = 2n\times n$
d’où $S_n = n\times n$ .

De même, les deux autres situations proposées peuvent mettre en évidence l’intérêt des nombres relatifs et du calcul algébrique.

Autres pistes

En poussant les cubes dans un coin, on peut faire les figures avec wisweb (cliquer sur le quadrillage de gauche pour faire apparaitre des cubes).

Personne à contacter pour cette activité : Marcel COMBÈS

En visitant la page http://maths.ac-amiens.fr/209-cubes.html, vous pourrez télécharger ces documents :

Rallye 2007 « mathématiques sans frontières », (PDF - 716.6 kio)