Mathématiques

Double distributivité

Niveau 3e ; Tableur - Calculatrice

mercredi, 21 mars 2012

http://maths.ac-amiens.fr/218-double-distributivite.html

Facile

Utilisation d’un vidéo-projecteur

En classe entière

Présentation de l’activité

L’activité commence par une séance de travaux dirigés sur le calcul numérique.

Calculer les valeurs des expressions :

lorsque :

1. a = 10
2. a = -10
3. a=0,3
4. a=

On constate sur les exemples calculés que les nombres E, F et G semblent avoir une différence constante.
Cette conjecture est faite grâce au tableur, utilisé collectivement.
La preuve est assurée par le calcul littéral, ce qui permet de retravailler les techniques vues en classe de quatrième.

Public / Niveau

Classe de troisième

Objectifs

• Réactiver la règle et la technique de double-distributivité.
• Réactiver la règle et la technique de suppression d’une parenthèse précédée d’un signe -.
• Retravailler le calcul numérique (nombres décimaux relatifs, nombres en écriture fractionnaire, priorités opératoires).

Objectifs secondaires :

• Retravailler le passage du numérique au littéral et utiliser le calcul littéral comme moyen de preuve.
• Former la différence de deux nombres pour prouver une égalité (a = b + k si et seulement si a - b = k).

Durée

Durée totale : 1 heure.

Ce qui a été fait avant

Rien (les pré-requis sont de niveau quatrième).

Notions réinvesties

• Calcul numérique sur les nombres décimaux relatifs et sur les nombres en écriture fractionnaire.
• Calcul littéral de quatrième

Déroulement de l’activité

Étape 1 : Réactivation des priorités opératoires et des techniques de calcul (20 minutes)

L’énoncé du travail est écrit au tableau ou projeté ou distribué aux élèves.

On peut commencer ce travail en fin d’heure et donner quelques calculs à préparer à la maison ou le commencer en début d’heure mais dans ce cas, il ne faut pas avoir d’exercices à corriger.

Pendant que les élèves travaillent, un transparent de correction avec toutes les réponses rédigées est projeté.

On réexplique le contrat de travail :

• On doit chercher avant de regarder la correction. La correction est là pour voir si on a juste et comment rédiger ou pour aider à trouver ses erreurs.
• On fait le maximum de calculs mais on les fait au maximum. Il vaut mieux en faire la moitié en ayant trouvé ses erreurs que la totalité en ayant des erreurs ou en ayant recopié la solution.
• Tout le monde n’avance pas à la même vitesse et il est possible que tous les élèves ne fassent pas tous les calculs. On peut éventuellement donner le reste en travail à la maison.
• Calculatrice autorisée de manière “raisonnable” (Par exemple, au plus deux utilisations par calcul ou uniquement pour faire les opérations qui sont “trop difficiles”).

Le professeur est disponible pour circuler et apporter des aides individuelles sur les erreurs et les méthodes.
Quelques points de méthodes sur les calculs sont faits collectivement.
Si on a accès à une salle informatique ou à des ordinateurs dans la classe, on peut très avantageusement utiliser « Le vérificateur d’égalités ».

Les exigences peuvent être différenciées : les élèves performants font tous les calculs, les élèves qui sont plus en difficultés ne font pas les calculs pour toutes les valeurs de a ou peuvent utiliser un nombre plus important de fois la calculatrice.
La première valeur (a = 10) est simple et met en confiance les élèves plus faibles.

On peut gagner du temps si on fait préparer des calculs à la maison, mais pas pour les 4 valeurs de a. Sinon on ne peut pas revenir efficacement sur les problèmes de priorités, de règles des signes, de mise au même dénominateur.

Lorsque la durée choisie par le professeur pour la partie travaux dirigés est écoulée, le professeur arrête cette première phase.

Étape 2 : Réactivation de la double-distributivité (35 minutes)

Le professeur dispose d’un ordinateur et d’un vidéo-projecteur avec la feuille de calcul ouverte.

On utilise le tableur pour vérifier les résultats de tous les calculs faits dans la séance de travaux dirigés.
Au passage, on revoit la saisie d’une formule dans un tableur.

• On saisit collectivement la formule dans B2.
  On peut accepter et même induire (3*10-4)*(6*10+5) (avec ou sans le = suivant l’expertise des élèves, si on veut rappeler encore une fois que « dans un tableur, toute formule commence par = ») et changer la valeur de A2. Cela est sans effet sur B2, alors que C2 change, ce qui renforce la nécessité d’entrer une « variable » dans la formule. La formule déjà écrite dans C2 peut permettre de retrouver le problème du non-changement de B2.

• On saisit collectivement la formule dans B2 : =(3*A2-4)*(6*A2+5) puis on recopie vers le bas.

• On demande aux élève d’écrire sur leur cahier la formule à saisir dans D2 pour faire calculer G.
  On saisit ensuite collectivement la formule dans D2 : =18*A2*A2-9*A2-10 puis on recopie vers le bas.

• On recopie C2 vers le bas pour avoir le tableau des résultats sous les yeux.

Nouvelle consigne : « Examiner les résultats et trouver des choses à dire »

• Les élèves recherchent en général de la proportionnalité.
  On peut l’éliminer facilement avec les lignes 2 et 3 ().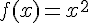

• L’écart constant apparaît (avec éventuellement un peu d’aide du professeur).
  Induire l’étude de G – E (il n’y aura que E à développer)
  En E2, on entre =D2-E2 et on recopie vers le bas. On conjecture que G – E = 10.

• On prouve, collectivement, à l’aide du calcul littéral que G – E = 10.
  Le professeur écrit au tableau :
  • On développe E : révision de la double-distribution,
  • On écrit G – E,
  • On revoit la règle de suppression de parenthèses et la réduction d’écritures littérales.

On peut effacer ou cacher le tableau avant que les élèves ne recopient et leur demander de refaire ce travail sur leur cahier ou attendre l’étape suivante suivant le temps disponible.

• On examine F – E (retour sur le tableur) et on conjecture que F – E = -8.

• Les élèves prouvent eux-même que F – E = -8 par le calcul littéral :
  • Ils développent E eux-mêmes : révision de la double-distribution,
  • Ils développent F : révision de la simple-distribution,
  • Ils écrivent et calculent F – E : règle de suppression de parenthèses et réduction d’écritures.

Fichier tableur

format Excel - 15 kio

Apport des TICE

• Le tableur permet de travailler le passage du numérique au littéral en travaillant sur la notion de variable.
• Le tableur permet de conjecturer que l’écart entre deux expressions est constante et de passer à l’écriture de la différence.

Personne à contacter pour cette activité : Philippe PICART