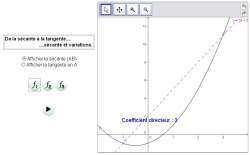
De la sécante à la tangente
- On introduit la notion de tangente comme position limite des sécantes.
- On peut alors regarder la limite du coefficient directeur.
- En déplaçant le point de tangence, on peut conjecturer le lien entre le signe du nombre dérivé et les variations de la fonction.
