Mathématiques

Le carré dans le triangle

Niveau 4e - 3e - 2nde - 1ère - Terminale ; Géométrie dynamique - Tableur - Calcul formel

lundi, 27 février 2012

http://maths.ac-amiens.fr/139-le-carre-dans-le-triangle.html

Facile

Utilisation d’un vidéo-projecteur

En classe entière

Présentation de l’activité

Quelles sont les dimensions (exactes) du carré inscrit dans ce triangle dont les dimensions sont données ci-contre ?

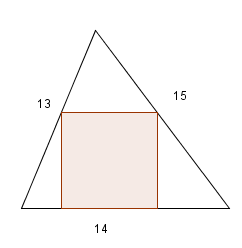
Public / Niveau

Testé en seconde

Durée

Travail maison + Une séance d’une heure

Objectifs

Chercher un problème de mathématiques
Travail sur les fonctions affines

Déroulement de l’activité

Le problème s’est déroulé en plusieurs phases :

Le problème est donné en exercice (sur le cahier) la veille.
Quelques idées :
- Des tracés du triangle, mais difficile de faire le carré.
- 2 élèves ont utilisé GeoGebra et ont imprimé la feuille.
- On a donc des propositions de valeurs, approchées (6,46 en zoomant).

Le professeur construit à partir d’une feuille blanche la figure au TBI.
- On construit la figure par « libération de contrainte », c’est à dire que l’on place un point sur le segment de 14 et que l’on construit à partir de là, un rectangle, que l’on va déformer pour qu’il devienne le plus proche possible d’un carré.

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

Question : Peut-on trouver une formule donnant la longueur du rectangle en fonction de sa largeur ?

Idée : Tracer la courbe de j en fonction de i sur la figure

A l’aide du GéoTableur, on capture des valeurs de i et j, et on les exporte dans un tableur.
- On trace alors depuis le tableur un nuage de points, ils semblent alignés.
- On peut alors tracer la courbe de tendance, et même obtenir son équation.
- L’équation ne “tombe pas juste”, en étudiant les « conditions aux bords », on trouve alors que l’on a 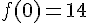et .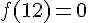
- On arrive alors à l’expression 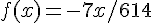et il restera à résoudre .

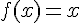Utilisation animée de GeoTableur format Flash - 1.9 Mio

Le point sur le problème : que reste-il à démontrer (par ordre de difficulté) ?
- Q3 : Résoudre .
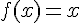- Q1 : Montrer que la hauteur du triangle mesure 12.
- Q2 : Prouver que la fonction est bien affine et que son expression est .
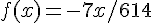  Les élèves travaillent par groupes de 2 ou 3 formés par le professeur.
  Certains groupes ne font que la question 3, d’autres la 1 aussi (la hauteur ayant été tracée, cela simplifie l’exercice). Avec de l’aide certains arrivent aussi à prouver la question 2.
  À la fin de l’heure, les élèves rendent une copie par groupe.

Le cours suivant :
- Retour sur les copies qui ont été sélectionnées et scannées.
- Les élèves expliquent leurs démarches.

Apport des TICE

L’aide de l’outil permet de passer des difficultés techniques.
En utilisant intelligemment l’outil, et avec quelques raisonnements simples, on arrive à la réponse exacte de 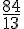$\frac{84}{13}$ qui peut sembler inaccessible dans un premier temps.

D’autres pistes

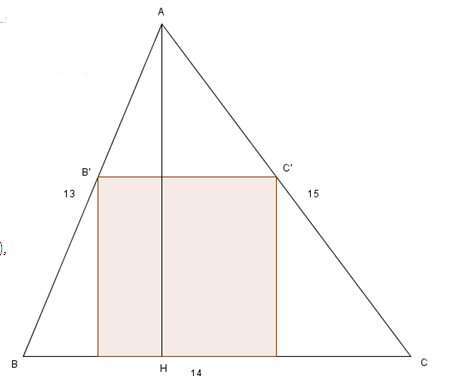
Avec les points définis ci-dessus, on note , et .

Calcul de h :
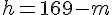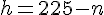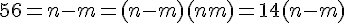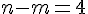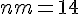En appliquant le théorème de Pythagore aux triangles ABH et ACH, on a : et , d’où donc et et et .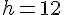

Calcul de la longueur du côté :
Comme les triangles ABC et AB’C’ sont semblables, on a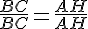 $\frac{BC}{B’C’}=\frac{AH}{AH’}$ , ce qui donne en notant 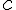, le côté du carré : 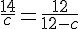$\frac{14}{c}=\frac{12}{12 - c}$ , d’où $c=\frac{84}{13}$ .

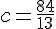D’autres idées extraites de copies d’élèves de terminale S, sans TICE : Al Kashi, des équations surprenantes mais correctes.

Copies d’élèves de terminale S format PDF - 737.6 kio

Remarque :avec ces notations, on a la relation 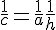$\frac{1}{c}=\frac{1}{a}+\frac{1}{h}$ , formule qui reste d’ailleurs valable dans le cas général.

Personne à contacter pour cette activité : Vincent MAILLE

En visitant la page http://maths.ac-amiens.fr/139-le-carre-dans-le-triangle.html, vous pourrez télécharger ces documents :

Fichier GeoGebra, (Fichier GeoGebra - 1.7 kio)