Mathématiques
Le pré et la chèvre
Niveau 3e - 2nde ; Tableur
lundi, 27 février 2012
http://maths.ac-amiens.fr/156-le-pre-et-la-chevre.html
Relativement facile
Manipulation de l’ordinateur
En groupe
Présentation de l’activité
Une personne possède un pré de forme carrée de 10m de côté.
Il attache une chèvre par une corde reliée à un piquet planté au milieu d’un des côtés.
Il souhaite que la chèvre broute une surface d’aire égale à la moitié de l’aire du pré.
Quelle longueur de corde doit-il laisser ?
Public / Niveau
- Travail en binôme en classe de seconde "expérimentale" (élèves en grosses difficultés)
- Réalisable en collège (à partir de la 4ème si les élèves ont l’habitude d’utiliser le tableur)
Ce qui a été fait avant
Séance réalisée en fin d’année, le programme de seconde est terminé, les élèves ont pas mal manipulé durant l’année l’outil TICE.
Thèmes abordés
- Pythagore.
- Calcul de l’aire d’un secteur angulaire.
- Trigonométrie.
Déroulement de l’activité
Le problème a été traité sur 3 séances d’une heure.
Séance 1 : Non TICE
- On entre dans le problème avec une version plus simple du problème posé :
Une personne possède un pré de forme carrée de 10m de côté.
Il attache une chèvre par une corde reliée à un piquet planté au milieu d’un des côtés.
- Quelle surface la chèvre peut-elle brouter si la corde mesure 4m ?
- Quelle surface la chèvre peut-elle brouter si la corde mesure 6m ?
Ici, pas besoin de TICE pour s’approprier le problème (même si le demi-disque ne vient pas tout de suite pour tous).
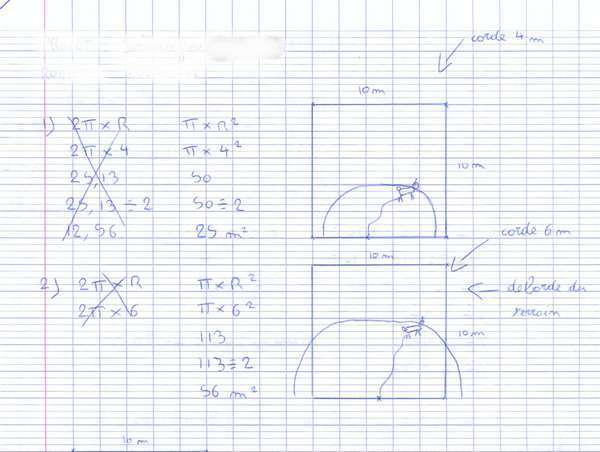
- Évidement, le problème apparait pour la deuxième question.
Je demande alors aux élèves de réfléchir à une technique pour calculer l’aire. Plusieurs découpages sont proposés :
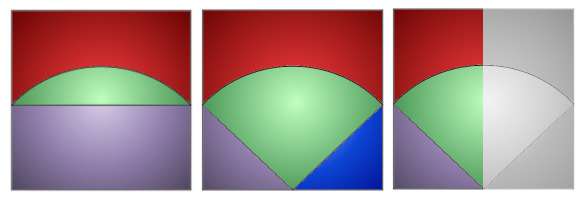
Le premier découpage est écarté, car aucune solution pour calculer l’aire verte ne semble évidente.
La plupart des binômes travaillent sur la deuxième proposition : la difficulté est relative, car les élèves ont été confrontés au scénario « La courroie » trois semaines avant. Le calcul de l’aire du secteur angulaire est plus facile.
- Tous les élèves ne finissent pas dans l’heure.
Séance 2 : Salle informatique
- On revient sur les idées de la séance précédente et les étapes de calcul.
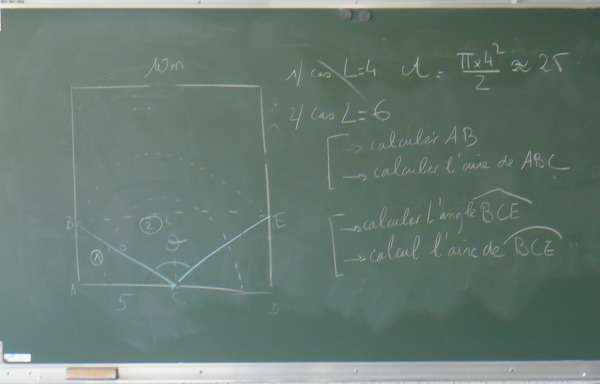
- Ceux qui n’ont pas fini le calcul de la précédente séance terminent sur feuille, les autres passent à la question qui nous intéresse :
Il souhaite que la chèvre broute une surface d’aire égale à la moitié de l’aire du pré. Quelle longueur de corde doit-il laisser ?
Les remarques des élèves sont : « Déjà, on sait que c’est plus que 6 mètres », « On peut faire des essais », « Oui, mais ça va être super long ! ».
- Je propose alors aux élèves « d’apprendre au tableur », comment faire, en travaillant étape par étape. Ensuite, il suffira d’essayer des valeurs pour trouver.
Voici un exemple de fichier réalisé par un groupe :
-
format Excel - 46.5 kio
Les élèves vérifient leurs formule avec L=4 et L=6 qu’ils ont calculé.
- À la fin de la séance, tous les élèves ont trouvé l’aire pour L=6 (ce qui est déjà bien), une bonne moitié travaille sur le tableur et un groupe a fini.
Séance 3 : Prolongements
- Les élèves terminent leurs fichiers. On cherche le résultat à
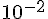 près.
près.
- Pour ceux qui ont fini, je propose un prolongement, puis un autre :
- Quelle doit être la longueur minimale de la corde pour que la chèvre puisse brouter tout le pré ?
- Tracer la courbe représentant la fonction qui donne l’aire en fonction de la longueur de la corde sur l’intervalle [0 ; 15].
Deux binômes arrivent au bout des prolongements.
-
format Excel - 299.5 kio
Aides apportées
Les aides techniques sont données au fur et à mesure des demandes et sont écrites au tableau pour la classe.
En particulier, le problème de conversion d’unité prévisible. Même en 2009 où le radian était encore au programme en seconde, j’avais donné la fonction “DEGRES” pour convertir les radians en degrés.

Fichiers utiles
Une figure sous GeoGebra pour illustrer le problème, mais qui ne m’a pas servi.
-
format Fichier GeoGebra - 3.2 kio
Apport des TICE
Répondre à un problème que je ne sais pas faire autrement.
Personne à contacter pour cette activité : Vincent MAILLE