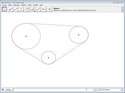
La courroie

 Présentation de l’activité

Le but de cette activité est d’utiliser un logiciel de géométrie dynamique dans l’objectif de dessiner une courroie puis de calculer sa longueur.

 Public / Niveau

Testé en seconde

 Objectifs

• Utiliser l’outil logiciel et les mathématiques dans un problème concret.
• Réinvestir plusieurs notions étudiées au collège dans la résolution de ce problème.

 Durée

• 1 séance d’une heure en salle informatique pour le dessin de la courroie.
• 1 séance d’une heure trente en classe pour le calcul de la longueur.

 Notions réinvesties

• Tangente à un cercle.
• Théorèmes de Thalès et de Pythagore.
• Angles et cosinus.
• Périmètre d’un cercle.
• Proportionnalité.

 Ce qui a été fait avant

Cette séance s’est déroulée sans cours préalable hormis des rappels sur la géométrie étudiée au collège.

 Déroulement de l’activité

• [55 min] : Pas de grandes difficultés hormis pour faire afficher la longueur de la courroie.
  La construction est assez longue pour obtenir clairement la courroie.

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

• [90 min] : Démonstration de la longueur.
  Le calcul des longueurs BC, FC et DC a bien été abordé (Théorèmes de Thalès et de Pythagore) mais a pris du temps.
  Plus de difficulté pour les arcs avec la formule du cosinus puis le calcul de l’arc proprement dit (par proportionnalité).
  La partie calcul a été assez longue car j’ai laissé les élèves travailler en petits groupes et vérifier avec le logiciel de géométrie dynamique, l’exactitude de leurs calculs à chaque étape.

Les groupes les plus rapides ont terminé en un peu plus d’une heure, pour les plus longs, ça a pris 1 h 30 environ mais ils ont tous terminé.

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

• Utilisation d’un logiciel de géométrie dynamique pour résoudre au moins graphiquement un problème donné.
• Utilisation du logiciel pour vérifier les étapes de calcul.

 Prolongements possibles

• Fixer deux paramètres, rayons des cercles par exemple, et déterminer l’entraxe pour une longueur donné de la courroie (résolution graphique avec le logiciel de géométrie dynamique ou avec un tableur en rentrant les formules de calculs).

• Dessin d’une courroie reliant trois cercles au lieu de deux (plus utilisée en mécanique).

Fichier GeoGebra

format Fichier GeoGebra - 3.6 kio

• Constitution d’un dossier bilan reprenant les séances informatiques, un prolongement parmi les deux précédents et de la documentation.

 Évaluation

Évaluation possible à 3 niveaux :

• Informatique : Réalisation de la figure.
• Mathématique : Démonstration de la longueur.
• Dossier : J’ai demandé aux élèves de me faire un petit dossier reprenant la figure, les calculs, un prolongement et de la documentation sur la courroie.

Exemple de dossier :

 Fichiers utiles

Le fichier de présentation de l’activité :

Présentation de l’activité format PDF - 140 kio

Présentation de l’activité format OpenDocument Text - 116 kio