Mathématiques
Une introduction au calcul intégral
Niveau Terminale S ; Géométrie dynamique - Tableur - Calcul formel
mercredi, 7 mars 2012
http://maths.ac-amiens.fr/192-une-introduction-au-calcul-integral.html
Facile
Utilisation d’un vidéo-projecteur
En classe entière
Présentation de l’activité
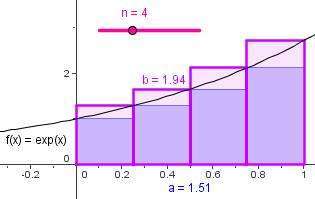
Calcul de la valeur exacte de l’aire comprise entre la courbe de la fonction exponentielle et l’axe des abscisses, entre 0 et 1.
Public / Niveau
Terminale S ou Terminale ES
Prérequis
- Étude des suites géométriques (en particulier, le calcul de la somme de termes consécutifs).
- Connaissance de la fonction exponentielle (définition et limites).
Déroulement de l’activité
- On utilise la méthode des rectangles pour d’abord encadrer l’aire du domaine choisi.
- Éventuellement, on utilise un tableur :
- D’une part, la coïncidence avec les résultats de GeoGebra par exemple avec n=10, permet de confirmer la programmation du tableur,
- D’autre part, la recherche d’un encadrement plus fin peut suggérer l’idée de passage à la limite.
- L’aire exacte peut être calculée comme limite de la somme des termes d’une suite géométrique de raison
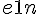 .
. - Le résultat des calculs peut être confirmé sur Xcas en ligne (calcul d’une somme infinie, intégrale d’une fonction).
- On peut alors donner définir l’intégrale d’une fonction positive sur un intervalle, ainsi que celle des suites adjacentes.
Fichiers utiles
- Le fichier tableur :
-
format Excel - 14.5 kio
- Le diaporama de la séance :
-
format PDF - 236.8 kio
Utilisation de Xcas en ligne
| Étape | Instruction à entrer dans la console | Expression mathématique | Valeur retournée par Xcas |
| 1 | sum((exp(1))^(k/n),k,1,2) | Calculer 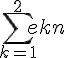 |
|
| 2 | sum((exp(1))^(k/n),k,0,n-1) | Calculer 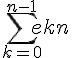 |
|
| 3 | normal(sum((exp(1))^(k/n),k,0,n-1)) | Simplifier 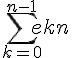 |
|
| 4 | limit(normal(sum((exp(1))^(k/n),k,0,n-1)),n=(+(infinity))) | Calculer |
|
| 5 | limit(1/n*normal(sum((exp(1))^(k/n),k,0,n-1)),n=(+(infinity))) | Calculer |
e1 - 1 |
| 6 | integrate(exp(x),x,0,1) | Calculer 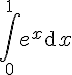 |
e1 - 1 |
Fichier de restauration (module console) de Xcas en ligne :
-
format Texte - 1.2 kio
Apport des TICE
- La figure dynamique permet de rendre visible l’encadrement par des sommes d’aires de rectangles, de suggérer le passage à la limite.
- Le
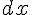 de l’intégrale prend un sens : c’est la largeur commune de tous les rectangles le long de l’axe des
de l’intégrale prend un sens : c’est la largeur commune de tous les rectangles le long de l’axe des 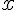 .
. - Les suites adjacentes s’introduisent tout à fait naturellement, et le dynamisme de la figure permet aux élèves de retenir plus facilement les critères.
- Le recours au tableur peut renforcer l’idée de passage à la limite.
- L’utilisation du calcul formel en ligne pour la sommation des aires peut guider les élèves vers la somme de termes consécutifs d’une suite géométrique, et fournir ensuite un moyen de vérification des calculs faits à la main.
Il peut resservir pour vérifier un travail personnel lors d’un prolongement.
Prolongements possibles
Dès que le raisonnement par récurrence a été étudié pour calculer la somme des carrés de 1 à n, on peut demander aux élèves de calculer l’aire sous une parabole.
Personne à contacter pour cette activité : René SOLEIL
En visitant la page http://maths.ac-amiens.fr/192-une-introduction-au-calcul-integral.html, vous pourrez télécharger ces documents :
- Fichier GeoGebra, (Fichier GeoGebra - 1 kio)