Mathématiques
Tour de magie n°3 : Le mentaliste
Cycle 4 (4ème et 3ème) ; débat
mercredi, 5 juin 2019
http://maths.ac-amiens.fr/501-tour-de-magie-no3-le-mentaliste.html
Activité produite dans le cadre des travaux académiques mutualisés 2018-2019.
Auteur : François Delannoy
Introduction :
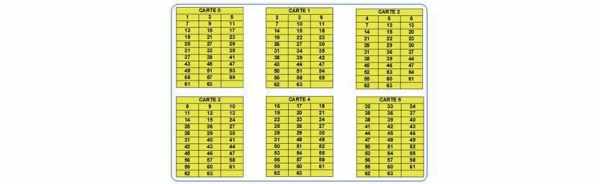
Des nombres de 1 à 63 sont écrits sur 6 cartes numérotées de 0 à 5.
- L’élève choisis un nombre entre 1 et 63 et l’écrit sur une feuille.
- Puis il indique au mathémagicien sur quelles cartes son nombre apparaît.
Alors de manière quasi-instantanée, le magicien est capable de retrouver le nombre de l’élève en connaissant uniquement le numéro des cartes sur lesquelles il apparaît (et sans même regarder les cartes).
Comment est-ce possible ?
Les activités suivantes sont tirées d’un articles de Computer Science Unplugged et d’un scenario de l’IREM de Clermont-Ferrand.
| Exemple(s) de scénario | Tour de magie |
| Niveau(x) concerné(s) | Cycle 4 (4ème et 3ème) |
| Séances préalables | Notion de puissances Écriture en binaire |
| Objectifs | Faire découvrir l’écriture binaire au travers d’activités ludiques. |
| Compétences visées | Chercher : S’engager dans une démarche scientifique, observer, questionner, manipuler, expérimenter (sur une feuille de papier, avec des objets, à l’aide de logiciels), Communiquer : Expliquer à l’oral ou à l’écrit (sa démarche, son raisonnement, un calcul ), comprendre les explications d’un autre et argumenter dans l’échange. Raisonner : Mener collectivement une investigation en sachant prendre en compte le point de vue d’autrui. . Fonder et défendre ses jugements en s’appuyant sur des résultats établis et sur sa maîtrise de l’argumentation |
Détail de la séance :
Une première approche :
En guise d’introduction, l’enseignant effectue le tour en classe.
Le déroulement :
L’enseignant présente aux élèves les 6 cartes sur lesquelles sont inscrits des nombres entre 1 et 63.
Il est demandé aux élèves de choisir secrètement un nombre, puis d’observer sur quelles cartes leur nombre est présent.
Un élève est interrogé, indique les cartes contenant son nombre (sans communiquer son nombre).
L’enseignant révèle le nombre de l’élève instantanément.
(Il arrive régulièrement qu’un élève se trompe et oublie d’indiquer l‘une des cartes. En cas de mauvaise réponse, il pourra être demandé à l’élève de vérifier que les cartes nommées sont correctes, ce qui permettra à l’enseignant de vérifier ses calculs …)
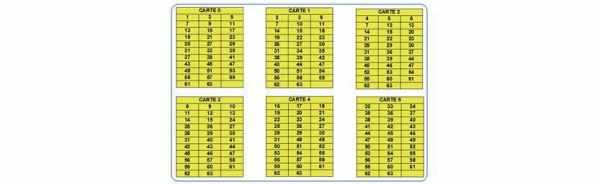
Le mécanisme du tour (secret) :
Chaque nombre entier entre 1 et 63 possède une décomposition en binaire qui est unique (en 6 bits).
La répartition des nombres sur les cartes correspond à cette décomposition binaire.
Pour retrouver le nombre secret connaissant le numéro des cartes, il suffit d’ajouter la première valeur de chacune des cartes nommées par l’élève.
Exemple : L’élève indique les cartes 0, 2, 3, 5.
L’enseignant regarde la première valeur présente sur chacune des cartes citées : Ici le 1 (carte 0), le 4 (carte 2), le 8 (carte 3) et le 32(carte 5).
Il calcule ensuite leur somme 1+4+8+32=45. Il a trouvé le nombre secret.
En effet, 45=1x2^0+0x2^1+1x2^2+1x2^3+0x2^4+1x2^5, d’où sa décomposition en binaire 101101.
Une fois le tour effectué, l’enseignant recueille les premières conjectures des élèves.
Découverte de l’écriture binaire : le jeu de cartes à points.
Découverte des puissances de 2.
L’enseignant dispose au tableau des cartes où figurent la représentation des premières puissances de 2 puis présente un exemple



Retour sur le tour de magie :
L’enseignant effectue une nouvelle fois le tour de magie. Les élèves sont ensuite amenés à en débattre afin de trouver la clé du tour.
Certains font le lien entre la disposition des nombres écrits sur les cartes et leur décomposition en binaire.
Il pourra ensuite leur être demandé de formaliser l’explication du tour à l’écrit par binôme, dans le but de vérifier que l’ensemble de la classe a bien compris le fonctionnement du tour.
L’élève mathémagicien :
Après explication du tour, les rôles sont inversés. L’enseignant choisit secrètement un nombre, indique les cartes sur lesquelles il est présent. Les élèves ont alors à déterminer le nombre choisi par l’enseignant.
Fichiers utiles
-
format PDF - 1.3 Mio
-
format PDF - 1.1 Mio
-
format PDF - 91 kio
-
format PDF - 22.4 kio
-
format PDF - 1.8 Mio
-
format PDF - 2.2 Mio
-
format PDF - 20.6 kio
-
format PDF - 141.9 kio