Mathématiques

Optimisation

Niveau 1ère S - Terminale S ; Géométrie dynamique

lundi, 27 février 2012

http://maths.ac-amiens.fr/147-optimisation.html

Facile

Manipulation de l’ordinateur

En groupe

Présentation de l’activité

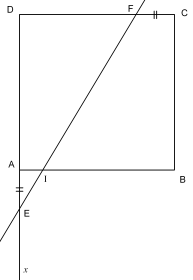
Soit ABCD un carré de côté 1.
E appartient à la demi-droite [Ax), F appartient au segment [DC] et ces deux points sont tels que AE = CF.
I est le point d’intersection des droites (AB) et (EF).

Déterminer la position du point E pour que la distance AI soit maximale.
Quelle est la position du point E qui rend l’aire du triangle AIE maximale ?

Public / Niveau

Première S

Objectifs

Conjecturer, à l’aide d’un logiciel de géométrie dynamique, les positions d’un point qui rendent une distance puis une aire maximales.
« Se rendre compte » que le logiciel ne fait pas tout, qu’il donne une valeur approchée … et qu’il faudra compléter cette première phase par l’obtention de valeurs exactes !

Ce qui a été fait avant

Dérivation et applications de la dérivation

Déroulement de l’activité

Exercice donné à faire à la maison :

Les élèves ont une dizaine de jours pour m’envoyer la figure sachant que si elle n’est pas correcte, je la renvoie en la déformant ou en faisant une remarque appropriée.
Ils peuvent à nouveau la rectifier ou non.
On corrige en classe à l’aide du vidéo-projecteur et en utilisant des fichiers élèves judicieusement choisis puis on passe à l’étude de fonctions.
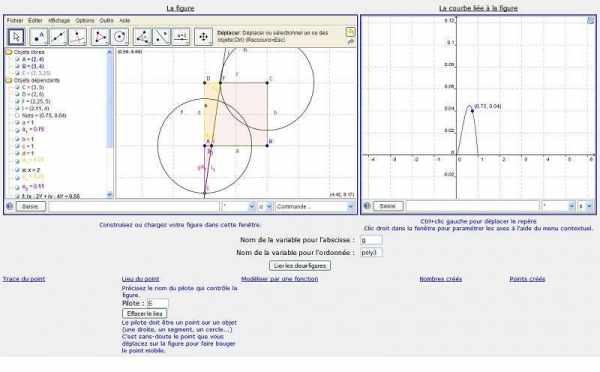
Utilisation du GéoTraceur par l’enseignant pour afficher la courbe sans avoir déterminé la fonction au préalable (possibilité d’utiliser le logiciel après avoir déterminé la fonction pour tracer la courbe, vérifier que la dérivée est correcte...).

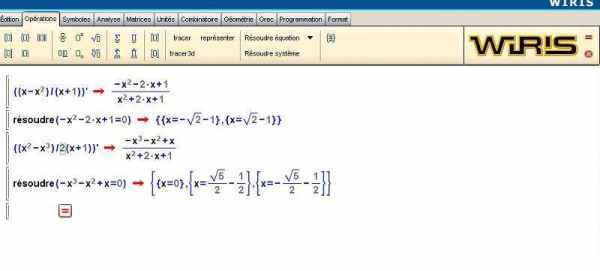
Utilisation possible d’un logiciel de calcul formel Wiris pour déterminer les dérivées.

Des remarques et échanges intéressants :

On peut bloquer le point E et ne pas laisser la demi droite car sinon F n’existe pas. Oui mais s’il n’est pas défini c’est pareil, ce qu’on veut c’est conjecturer.
On peut conjecturer 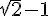$\sqrt{2}-1$ en trouvant 0,414 mais pour l’autre valeur $\frac{\sqrt{5}-1}{2}$ !
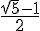Pas simple de créer un cercle avec un rayon variable (on préfère quand c’est fixe).
Pour voir les résultats quand on “bouge” sans regarder dans la fenêtre algèbre : utilisation de l’étiquette « Valeur », insertion d’un objet et insertion « mixte » pour certains avec demande à distance.

Fichiers utiles

L’énoncé papier

Énoncé papier format PDF - 21.7 kio

Énoncé papier format Word - 26.5 kio

Fichiers élèves

Exemple d’élève format Fichier GeoGebra - 1.7 kio

Exemple d’élève format Fichier GeoGebra - 1.8 kio

Exemple d’élève format Fichier GeoGebra - 1.9 kio

Copies d’élève format PDF - 152.9 kio

Apport des TICE

Optimisation avec utilisation d’un logiciel de géométrie dynamique.
Émission de conjecture à l’aide du logiciel et vérification des résultats.
Utilisation possible du calcul formel pour valider des résultats.

Personne à contacter pour cette activité : Guillaume MIANNAY