Mathématiques

Équations diophantiennes du second degré

Niveau Terminale S Spécialité ; Tableur

lundi, 27 février 2012

http://maths.ac-amiens.fr/151-equations-diophantiennes-du-second-degre.html

Facile

Manipulation de l’ordinateur

En groupe

Présentation de l’activité

Résoudre les équation diophantiennes et

Public/niveau

Terminale S spécialité

Objectif

Résolution d’une équation diophantienne.
Utilisation des références mixtes du tableur quand cela s’avère réellement utile.
Découverte de la mie en forme conditionnelle.

Déroulement de l’activité

Le sujet est écrit au tableau :

À l’aide du tableur, d’une calculatrice ou d’un logiciel de calcul formel, déterminez une décomposition en facteurs premier de 8633.
Résoudre dans $\mathbb{N}$ :
Résoudre dans $\mathbb{N}$ :

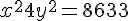
La première question ne pose pas de difficulté et peut être l’occasion de mettre en place un algorithme simple.
La deuxième question est mathématiquement simple. Ceux qui se lancent sur une recherche par ordinateur se trouvent rapidement bloqués devant l’infinité de possibilités à tester.
Pour la troisième question, cette fois ci n’est pas simple mais on peut heureusement faire une majoration de x et y et programmer l’ensemble de solution.
Reste que si le nombre de possibilité est fini, il faut les retrouver parmi les $93\times47$ soit 4371 possibilités : L’usage d’une mise en forme conditionnelle et/ou d’un NB.SI peut alors grandement aider à repérer le solutions.

La question 3 sans les TICE

Question d’un élève : Peut-on résoudre cet exercice sans un ordinateur sous la main ?

Merci à Philippe DOMERGUE pour cette proposition de démarche alternative :

Développer (a² + b²)(c² + d²) puis (ac + bd)² + (bc - ad)².
Que remarque-t-on ?
On admettra que la remarque est valable aussi pour (ac - bd)² + (bc + ad)².
Écrire 89 sous la forme a² + b².
Écrire 93 sous la forme c² + d².
Achever la résolution du problème posé.

Apport des TICE

Résoudre la question 3 (dans le cas borné, le tableur permet de traiter tous les cas possibles).
Visualiser l’ensemble des solutions dans le cas réel.

Prolongements possibles

Représenter ces solutions dans 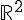$\mathbb{R}^2$ avec GeoGebra : il suffit de taper l’équation dans la barre de saisie en bas et à l’aide de la grille, donner du sens à la recherche des couples d’entiers.

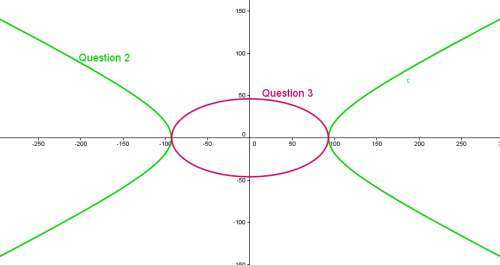
Discussion avec les élèves autour de la véracité d’une preuve par la machine.

Fichiers utiles

Exemple de réponse à la question 3 format Excel - 168.5 kio

Variante

Une activité proposée par Nicolas DANIEL.

Variante proposée par Nicolas DANIEL format PDF - 67.9 kio

Variante proposée par Nicolas DANIEL format LaTeX - 3.6 kio

Personne à contacter pour cette activité : Vincent MAILLE