Partager un carré en quatre triangles isocèles

 Présentation de l’activité

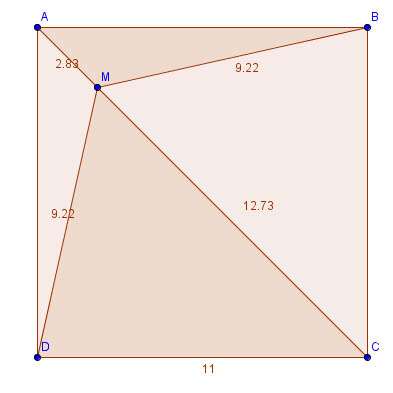
Il est facile de partager un carré en quatre triangles isocèles rectangles ou en quatre triangles rectangles non isocèles mais peut-on partager un carré en quatre triangles isocèles non rectangles ?

 Public / Niveau

Sixième

 Pré-requis

Les triangles particuliers ont pu être abordés dans différentes situations (construction, périmètre) dans les activités précédentes mais cela n’est pas obligatoire.
Toutefois, la connaissance de la construction au compas du triangle équilatéral ainsi que la propriété caractéristique des points d’un cercle peuvent être des éléments facilitant l’entrée dans les démonstrations qui seront explicitées en fin d’activité.

 Notions investies

Problème de recherche mettant en jeu les figures élémentaires de géométrie (carré, triangles particuliers, cercle) et leurs propriétés.

 Déroulement de l’activité

En travail personnel, les élèves sont sollicités pour trouver différentes manières de partager un carré en quatre parts identiques. Un point est fait quelques jours plus tard en début de séance sur les partages obtenus.

En général, trois partages sont obtenus :

• partage du carré en quatre carrés par les axes médians,
• partage du carré en quatre rectangles
• partage du carré en quatre triangles isocèles et rectangles par les diagonales.

On demande alors (sauf s’il a été obtenu) de continuer la recherche de façon à avoir quatre triangles rectangles non isocèles.
Un point est fait lors des séances suivantes.

On relance alors la recherche en demandant si on peut partager un carré en quatre triangles isocèles non rectangles mais pas forcément de même aire.

Lors de la mise en commun :

• soit aucune solution acceptable est proposée ; on peut relancer la recherche personnelle avec un indice tel que « il faut placer un point M à l’intérieur du carré » et attendre la séance suivante.
• soit une solution approchée est mise en exergue par au moins un élève.
  Dans ce cas, la « validation » relève en général de la géométrie perceptive pour les triangles « bien positionnés » et de la géométrie instrumentée pour les autres triangles ; cependant l’imprécision due au mesurage laisse un doute suffisant pour prolonger la réflexion.

On peut alors proposer aux élèves de retrouver cette solution à partir de la figure construite sur Geoplan et projetée au tableau avec un vidéo-projecteur.
Les élèves proposent rapidement de déplacer le point M pour qu’il soit sur la droite passant par les milieux de deux côtés opposés du carré. Pour faciliter ce positionnement du point M, on peut compléter la figure en traçant cette droite.
Ensuite, ils proposent de déplacer le point M sur cette droite de façon à obtenir la position attendue.
L’analyse des résultats met en évidence que l’un des triangles est équilatéral et permet donc d’envisager une construction (au compas) du point M qui peut être explicitée par le tracé d’un ou des deux cercles en jeu.

Cela sera alors l’occasion d’affiner la définition du triangle isocèle :

« Un triangle isocèle est un triangle qui a au moins deux côtés de même longueur. »

On peut alors envisager :

• la réalisation de la figure sur support papier :
  • construction d’un carré,
  • recherche au compas du point M,
  • tracé des quatre triangles.
• la démonstration du caractère isocèle des quatre triangles :
  • Pour trois d’entre eux, la propriété caractéristique des points du cercle et la transitivité de l’égalité y seront sollicitées et permettront une démonstration complète.
  • Pour le quatrième , c’est la présence d’un axe de symétrie (à admettre) qui permettra de justifier.

Le fait qu’ il y a quatre positions possibles du point M permettant d’obtenir le partage demandé.

 Fichiers utiles

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

Le fichier Geoplan représentant le carré partagé en quatre triangles avec affichages des mesures des côtés des quatre triangles.

Fichier Geoplan-Geospace

format Geoplan-Geospace - 3.7 kio

Le fichier Cabri permettant d’initier à la construction de puzzles dans le cadre par exemple d’un club mathématique.

Fichier Cabri Géométre

format Cabri Géométre - 3.2 kio

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

La modification instantanée, liée au déplacement du point M, de l’affichage des longueurs rend opérante la stratégie « par essai » pour approcher la (ou une) solution du problème.
Cette stratégie avec les instruments traditionnels (papier /crayon , règle …) peut entrainer une démobilisation.

Bien que l’utilisation du logiciel reste dans le domaine de la géométrie instrumentée, elle permet d’assurer une meilleure participation orale de l’ensemble des élèves , et d’envisager au cours de la recherche le tracé de certains des éléments de construction du point cherché.

 Prolongements possibles

On peut par exemple proposer aux élèves de construire la figure sur un logiciel de géométrie dynamique et leur permettre de découvrir la fonctionnalité de l’outil cercle pour reporter des longueurs et ainsi obtenir un programme de construction d’un carré sur un tel logiciel.

En classe de 5ème, on peut envisager d’évaluer le poids de chaque triangle. On pourra aussi chercher les mesures des angles de chacun des triangles et envisager de construire séparément les quatre triangles pour reconstituer sous forme d’un puzzle le carré.

En club mathématique, on peut envisager avec l’option « copier- coller » la construction d’un tel puzzle.