Etude d’un agorithme
Relativement facile
Utilisation d’un vidéo-projecteur
En classe entière
Présentation de l’activité
On a entré l’algorithme suivant avec Wiris.
Que fait ce programme lorsqu’un nombre n est donné ?
et appuyer sur = ou "CRTL + Entrée" pour l’exécuter et conjecturer.
Public / Niveau
Terminales S spécialité
Objectifs
- Étude d’un algorithme.
- Travail sur les nombres premiers de la forme
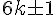 .
.
Durée
30 min
Prérequis
- Connaissance des nombres premiers
- Test de primalité
- Travail sur les congruences
Ce qui a été fait avant
Les élèves avaient déjà conçu des algorithmes de test de primalité classique :
- Calcul de PGCD par algorithme d’Euclide, sur tableur,
- Programme de calcul de modulo, sur calculatrice,
- Test de primalité classique en testant tous les diviseurs de 2 à
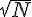 , sur tableur, calculatrice ou Wiris.
, sur tableur, calculatrice ou Wiris.
Déroulement de l’activité
Les élèves viennent modifier au tableau les valeurs de n.
La conjecture arrive assez rapidement.
Questions que l’on peut alors se poser :
- Quelles valeurs peut prendre le nombre
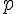 ?
?
- Quand
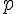 prend t-il la valeur 1 ?
prend t-il la valeur 1 ?
- Quand
- A quelle(s) condition(s) la boucle TANT QUE s’arrête-elle ?
- Tous les diviseurs sont-ils testés ?
- Les nombres a et b sont-il toujours premiers ?
Tous les diviseurs premiers sont-il testés ?- A-t-on
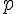 premier
premier 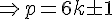 avec
avec 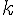 entier naturel strictement positif ?
entier naturel strictement positif ? - A-t-on
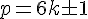 avec
avec 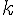 entier naturel strictement positif
entier naturel strictement positif 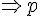 premier ?
premier ?
- A-t-on
On peut utiliser le tableur pour ces questions
Fichiers utiles
Une feuille avec le sujet :
|
|
Une page internet contenant l’algorithme Wiris :
-
format HTML - 2.2 kio
Apport des TICE Technologies de l’information et de la communication pour l’enseignement
- Exécuter un algorithme.
- Conjecturer sur la primalité des termes des suites
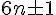
Prolongements possibles
On peut se poser d’autres questions comme :
- Que se passe-t-il si on remplace la première ligne
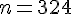 par :
par :
-
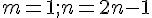 et que l’on fait varier
et que l’on fait varier 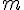 de 1 à 5 ?
de 1 à 5 ? -
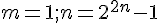 et que l’on fait varier
et que l’on fait varier 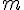 de 1 à 20 ?
de 1 à 20 ?
-
Pour information
Personne à contacter pour cette activité : Vincent MAILLE