La longueur de l’escargot de Pythagore
Relativement facile
Utilisation d’un vidéo-projecteur
En groupe
Présentation de l’activité
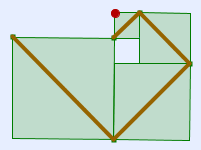
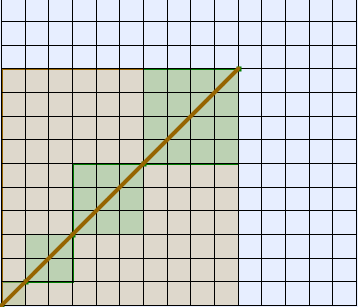
Quelle est la longueur de l’escargot de Pythagore (ligne marron ci-dessus) ?
Public / Niveau
Troisième
Objectifs
- Travailler les égalités
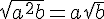 et
et 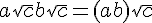
- Déstabiliser l’erreur
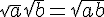
Ce qui a été fait avant
- Notion de racine carrée
- Compatibilité de la racine carrée avec la multiplication
Déroulement de l’activité
- Comme le nombre de carrés est variable (ici 4), on peut faire apparaître plus de carrés au début pour faire visualiser l’escargot puis en diminuer le nombre.
- La ligne brisée dont on cherche la longueur s’exprime comme une somme de nombres en écriture avec des radicaux :
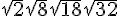 .
.
- La ligne brisée apparait comme une ligne droite, dont la longueur apparaît comme celle de la diagonale d’un grand carré :
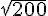
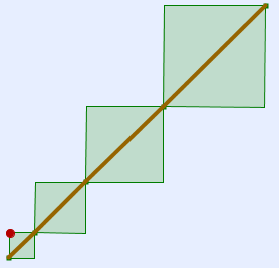
- Lorsque l’escargot est complétement déroulé, on fait apparaître le grand carré et le quadrillage pour calculer les longueurs des côtés des carrés.
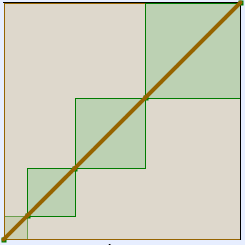
|
|
- Si pour l’élève la simplification de
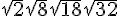 est
est 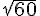 , on aboutit à une contradiction puisque la diagonale du grand carré mesure
, on aboutit à une contradiction puisque la diagonale du grand carré mesure 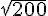 .
.
- On simplifie chaque diagonale de petits carrés, on réduit la somme puis on compare
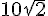 et
et 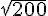 .
.
Aides possibles
- Il est possible de diminuer le nombre de carrés, éventuellement jusqu’à un pour faire apparaître la décomposition en somme de carrés et l’intervention du théorème de Pythagore.
- L’affichage du quadrillage aide à calculer les longueurs des côtés des carrés.
Apport des TICE Technologies de l’information et de la communication pour l’enseignement
- Figure dynamique avec curseur pour régler le nombre de carrés.
Pour information
Personne à contacter pour cette activité : Philippe PICART