Image d’un cercle

 Présentation de l’activité

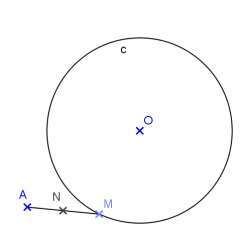
Soit C un cercle et A un point n’appartenant pas à C.

On place sur le cercle C, un point M, et on construit alors le point N sur le segment [AM] tel que AN = 0,5AM.

Quelle forme géométrique parcourt le point N lorsque le point M parcourt l’intégralité du cercle C ?

 Public / Niveau

Testé en seconde, réalisable en 3ème et 4ème.

 Séances préalables

Une séance non TICE Technologies de l’information et de la communication pour l’enseignement sans rapport avec le scénario, pour découvrir la formule de distance dans un repère orthonormé. Elle utilisait une illustration au vidéo-projecteur pour s’imprégner de l’interface du logiciel utilisé.

Côté mathématiques, ce problème est volontairement déconnecté du reste du cours, il ne met en jeu que des connaissances antérieures du collège.

 Objectifs

• Étudier le lieu d’un point.
• Revisiter les théorèmes de géométrie du collège :
  • Soit la droite des milieux, dans ces 2 utilisations.
  • Soit le théorème de Thalès et sa réciproque (que l’on peut forcer en prenant 1/3 ou 1/4 à la place de 1/2).

 Déroulement de l’activité

L’énoncé est écrit au tableau.

• Les élèves décident de faire la figure dynamique (il faut dire que l’on est en salle informatique).

• La figure arrive assez vite, le choix du rapport d’un demi permet une construction rapide en passant par le milieu.

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

• L’idée de la réponse (cercle) arrive aussi assez rapidement, pour les élèves ayant construit correctement la figure.
  Certains ont utilisé le point M pour construire le cercle C, de ce fait on ne peut pas déplacer M sans déformer le cercle.

• On demande alors de retrouver les éléments caractéristiques de ce cercle (centre et rayon).
  Cette fois-ci le bouton « Lieu d’un point » trouve tout son intérêt car il permet de visualiser le lieu du point au fur et à mesure que le cercle de départ est déformé.

 Prolongements

Pour les plus rapides, ou en devoir à la maison, on peut demander ce qu’il se passe si M ne se déplace plus sur un cercle, mais sur une droite.

Les conjectures sont assez rapides, les preuves un peu moins faciles, même si les notions mathématiques sont identiques.