Carré et triangle équilatéral de même périmètre

 Présentation de l’activité

Combien doit mesurer le côté du carré pour que le carré et le triangle équilatéral aient le même périmètre ?

 Public / Niveau

Troisième (tous niveaux), quatrième

 Objectifs

• Calcul littéral et mise en équation comme moyen de résoudre un problème.
• Apprendre à chercher.
• Distinction entre valeur exacte et valeur approchée.
• (Re-)découvrir le tableur.

 Ce qui a été fait avant

• Ce problème n’a pas été proposé en premier problème de mise en équation.
  D’autres problèmes avaient été résolus :
  • 1ère séquence de l’année : calculs de volumes, grandeurs produits et grandeurs quotients, en ayant recours à des lettres pour les calculs de volumes.
  • 2ème séquence de l’année : résolution de problème avec mise en équation.

• On en avait extrait des points méthodes pour la résolution de problème avec mise en équation (transition entre les deux séquences). Mais les élèves étaient très peu autonomes dans la mise en équation et manquaient de confiance en eux ou se contentaient d’essais peu aboutis.

 Remarques

• La solution n’est pas décimale (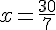) donc la méthode de recherche par essais-erreurs n’aboutit pas.
• Le choix de l’inconnue est à la charge de l’élève (induit par l’énoncé).
• On est amené à rejeter la mise en équation avec deux inconnues à cause d’un manque de technique.
• L’équation s’écrit assez facilement : « périmètre du carré = périmètre du triangle équilatéral ».
• Une petite révision de la distributivité au passage pour résoudre l’équation.

 Déroulement de l’activité

Séance 1 : 15 minutes avant la fin de l’heure

• À faire sur copie :
  • Travail individuel pendant 5 minutes.
  • Au bout de 5 minutes de recherche, discussion autorisée entre voisins pour échanger les idées et mieux comprendre l’énoncé.

• Ramassage des copies en fin d’heure.

• Travail maison pour les élèves : exercices d’entrainement à la résolution d’équation avec parenthèses.

• Travail maison pour le professeur : avant la séance suivant, relever les procédures et les débuts de recherche dans les copies (photographie de quelques extraits de copies).

Séance 2 : 20 minutes de recherche

• Projection des extraits de copies et bilan sur les procédures et les débuts de recherche.
  On précise les exigences en matières de rédaction : explication des essais réalisés et conclusion nécessaire de chaque essai.

• À l’aide de la figure dynamique, on s’approprie définitivement le problème et on précise qu’il a une solution (certains élèves en doutent).

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

• On encourage) la procédure essais-erreurs :
  • Faire comprendre aux élèves qu’ils ont droit à l’essai en mathématiques : les essais permettent de s’approprier le problème, les essais multiples sont le début de l’algébrisation.
  • Faire comprendre aux élèves qu’ils ont droit à l’erreur, que l’erreur ne doit pas être effacée mais qu’elle prouve une recherche et une réflexion.

• On relève les débuts d’algébrisation.
  Prévoir une feuille de problèmes supplémentaires pour les élèves ayant terminé la résolution du problème sous forme algébrique (ça arrive) et donner à finir à la maison pour les autres élèves.

Séance 3 :

• Retour rapide sur la figure dynamique pour relancer le problème.

• Ouverture d’une feuille de calcul tableur pour optimiser la procédure essais-erreurs et pour finalement rejeter cette procédure :
  • Feuille 1 : calcul unique.
    Formules mises au point collectivement. On (re-)voit comment on insère une formule dans un tableur.
  • Feuille 2 : calcul recopié vers le bas pour garder la trace des essais successifs.
    On améliore la détection des valeurs “bornes” en ajoutant une colonne faisant la différence entre les deux périmètres (on voit nettement apparaître les nombres négatifs).
  • Feuille 3 : calcul recopié vers le bas avec pas d’incrémentation paramétrable (feuille préparée par le professeur).
    On trouve “facilement” une valeur approchée jusqu’au dix-millième. Mais la procédure est reconnue comme longue et fastidieuse par les élèves.

Fichier tableur

format Excel - 16 kio

• On est TOUS d’accord sur la supériorité de la procédure algébrique.
  La mise en équation se fait à partir de la feuille de calcul du tableur. Il n’y a plus qu’à traduire les formules de calcul de périmètre avec au lieu de A2.
• On retrouve l’équation qui était sous notre nez depuis le début : « périmètre du carré = périmètre du triangle équilatéral »

 Évaluation

• Il est intéressant de donner ce type d’exercice sur feuille (non-noté) pour forcer les élèves à entrer dans la recherche et pour suivre leurs procédures de résolution.
• Les copies sont ramassées 2 fois par l’enseignant.
  Quelques copies manifestant l’engagement dans la recherche sont notées (note bonus sur 5 avec aucune note inférieure à 4/5 ou 5/5) pour valoriser la recherche et l’engagement et pas le résultat.

 Réinvestissements

• D’autres problèmes nécessitant une mise en équation seront donnés dans les séquences suivantes et en devoir maison.

• Réinvestissement proposé :
  Quelle doit être la largeur du rectangle pour que son périmètre soit égal au périmètre du triangle équilatéral ?

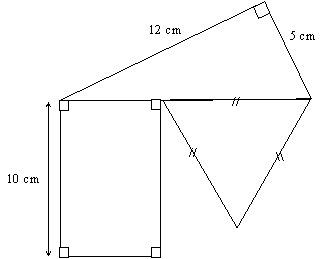
Utilisation du théorème de Pythagore pour trouver la longueur de l’hypoténuse : 13 cm.
Équation à résoudre : .
Solution :

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

• La figure dynamique fait comprendre qu’une quantité (le périmètre) varie en fonction d’une autre (la longueur du côté du triangle) : approche de l’initiation à la notion de fonction.
• La figure dynamique et ses fonctionnalités (affichage des périmètre et des longueurs) fait comprendre que le problème a une solution.
• La feuille tableur permet d’approcher la solution et l’approximation permet un travail sur les nombres décimaux (intercalation).
• La feuille tableur permet de faire apparaitre la procédure par essais-erreurs comme efficace (mais pénible) pour approcher la solution mais inopérante pour trouver la solution exacte.

 Variante

Si on souhaite accentuer le travail sur les valeurs exactes et sur la résolution d’équation ou si on craint que les élèves se découragent ou ne cherchent pas ou trouvent qu’une valeur approchée au dixième est bien suffisante, on peut proposer une première question facile :
« Pour quelle valeur le périmètre du triangle équilatéral est-il le triple du périmètre du carré ? »

Une fois cette question résolue sans ambiguïté on pose l’autre question :
« Pour quelle valeur le périmètre du triangle équilatéral est-il égal au périmètre du carré ? »

Comme l’énoncé semble plus facile que le premier (il n’y a pas de tiers), les élèves penseront que la solution doit être facile à trouver et seront plus volontaires pour la chercher.