Optimisation de l’aire d’un rectangle
Facile
Manipulation de l’ordinateur
En groupe
Présentation de l’activité
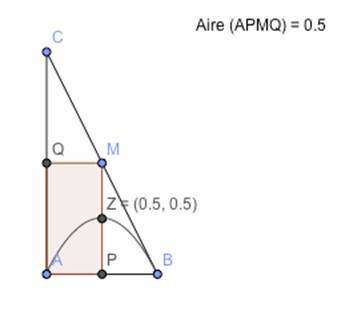
Q appartient à [AC], P appartient à [AB] et M appartient à [BC] tel que APMQ soit un rectangle.
Comment choisir M pour que l’aire du rectangle APMQ soit maximale ?
Public / Niveau
- Première S (utilisation du second degré)
- Possible aussi en Seconde (avec questions pour le second degré)
Durée
1 heure en demie classe : chaque élève dispose d’un ordinateur.
Objectifs
- Première étape : construction de la figure.
- Deuxième étape : conjecturer la position du point M.
- Troisième étape : démontrer le résultat conjecturé.
Ce qui a été fait avant
Cours sur le second degré.
Déroulement de l’activité
- Élèves : utilisation de GeoGebra pour construire la figure.
- Des élèves pensent au milieu P de [AB].
- Avec « polygone », on crée un polygone (ici un rectangle) dont l’aire s’affiche, il suffit de modifier la position de M et émettre la conjecture.
- Professeur :
- Utilisation d’un repère d’origine A et de
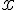 pour préciser la position de P.
pour préciser la position de P. - Utilisation du vidéo-projecteur : figure avec A(0 ;0), B(1 ;0) et C(0 ;2) puis ajout de la “trace activée” de Z(x ;Aire(x) ) qui permet d’appuyer la conjecture des élèves.
Possibilité d’exploiter la courbe obtenue avec la trace.
- Utilisation d’un repère d’origine A et de
Pour la preuve
- Équation de la droite (BC).
- Aire en fonction de x.
- Second degré et variations du trinôme.
Apport des TICE Technologies de l’information et de la communication pour l’enseignement
Créer un figure dynamique permettant de conjecturer le résultat attendu.
Pour information
Personne à contacter pour cette activité : Guillaume MIANNAY