Calcul d’un escalier

 Présentation de l’activité

C’est un problème ouvert :
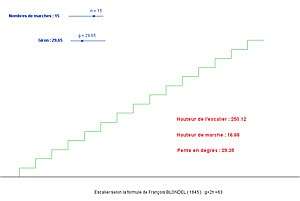
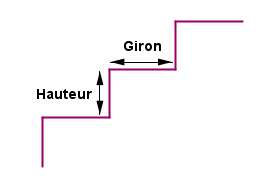
L’architecte François Blondel (1618-1686) est l’auteur d’une relation entre le giron (g) et la hauteur (h) d’une marche d’un escalier : g + 2h = 63, les dimensions étant données en cm.
Un tel escalier est agréable à monter pourvu qu’il respecte les normes modernes : le giron doit mesurer entre 24 et 32 cm et la hauteur d’une marche au maximum 18 cm. Ces normes sont valables pour un logement.

On veut construire un escalier de hauteur totale 2,70 m, répondant aux normes précitées.
Il peut y avoir plusieurs solutions ! Pour chaque cas possible, il faut :

1. Calculer le nombre de marches nécessaires ainsi que le giron et la hauteur des marches de cet escalier.
2. Calculer la pente de cet escalier.
3. Tracer l’escalier avec le logiciel GeoGebra.

 Public / Niveau

Testé en première STI Sciences et technologies industrielles , mais certainement utilisable dans beaucoup d’autres niveaux.

 Objectifs

Encore un exercice où l’objectif principal est de modéliser le problème.
Celui-ci se ramène a une équation à deux inconnues avec contraintes, ce qui risque de déstabiliser de nombreux élèves.
L’outil informatique s’impose de lui même : le tableur semble être une bonne solution, mais GeoGebra permet de tracer l’escalier, et au passage, de faire un bon exercice sur les coordonnées.

 Pré-requis

Des connaissances sur le tableur et GeoGebra.

 Déroulement de l’activité

L’idéal est de donner le problème brut aux élèves quelques jours avant la séance en salle informatique.
Beaucoup d’élèves ont bien du mal à écrire l’équation : nh=2,7 avec n entier naturel correspondant au nombre de marches et h la hauteur de chaque marche.

Une fois l’équation trouvée, le tableur s’impose pour beaucoup d’élèves, il leur faut une bonne demi-heure pour trouver les différentes solutions au problème.

La suite est plus délicate mais tellement plus enrichissante : il s’agit de tracer l’escalier avec GeoGbra en faisant varier le nombre de marches et le giron par curseurs, la hauteur des marches se déduisant du giron par la relation de Blondel. Il suffit ensuite de calculer et de faire afficher la hauteur totale et la pente de cet escalier par GeoGebra.
Un peu d’aide est parfois nécessaire pour trouver les coordonnées des extrémités des segments, et pour utiliser la commande « séquence » de GeoGebra.
Cette exercice est une belle occasion pour parler de suites numériques.

Fichier tableur format Excel - 17 kio

Fichier GeoGebra format Fichier GeoGebra - 1.4 kio

Un élève m’a demandé si les conditions sur le giron et la condition sur la hauteur de marche étaient bien compatibles. Excellente question qui permet de réinvestir les connaissances sur les inégalités.

 Fichiers utiles

Le fichier élèves :

Fichier élève format PDF - 11.6 kio

Fichier élève format Word - 32 kio

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

Ce problème n’est pas facile à résoudre sans l’outil informatique.
Le minimum étant le tableur mais GeoGebra, avec sa commande « séquence », permet de tracer facilement l’escalier, après avoir trouvé les coordonnées des extrémités des segments formant cet escalier.

Les curseurs permettent de faire varier le nombre de marches et le giron, ce qui permet de trouver rapidement toutes les solutions et de les visualiser.

L’utilisation de GeoGebra pour résoudre se problème permet aux élèves de mobiliser beaucoup de leurs connaissances.