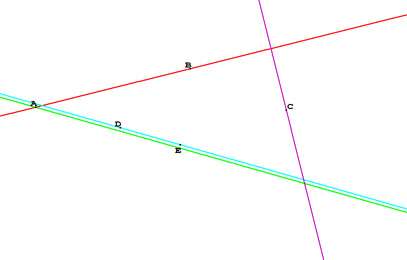
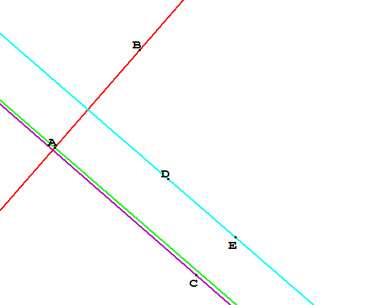
Recherche de configurations de points amenant des droites confondues

 Présentation de l’activité

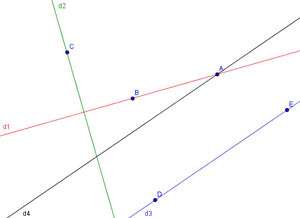
Cinq points “libres” A, B, C, D et E et quatre droites définies à partir de ces points par :

• 
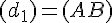
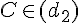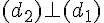
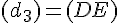
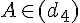• et
• 
• et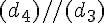

Peut-on avoir 2, 3 ou 4 des droites confondues ? Envisager toutes les solutions possibles.

 Public / Niveau

Activité initiale créée en 1998 et proposée régulièrement avec des adaptations et des évolutions en classe de sixième dans un collège en ZEP Zone d’éducation prioritaire .

 Pré-requis

• Notions élémentaires de géométrie (point, droite, points alignés).
• Reconnaissance de droites parallèles, perpendiculaires.
• Construction de droites perpendiculaires.

 Ce qui a été fait avant

Une première activité (les deux points cachés) permettant de poser les concepts de points et de droites ainsi que le vocabulaire lié à ces concepts.
Elle permet aussi de fixer une représentation mentale privilégiée de la notion de droites perpendiculaires à partir du modèle de droites perpendiculaires représenté sur papier calque et distribuée au cours de la séance à chaque élève.

Les compétences liées à la validation d’une solution possible à un problème ayant plusieurs contraintes y sont fortement sollicitées. Les élèves prennent conscience de la possible nécessité de prolonger le dessin des droites d’une figure pour obtenir la solution à un problème de recherche de points.

 Déroulement de l’activité

Séance 1 : En classe entière

• Analyse de la figure construite au tableau avant l’arrivée des élèves et distribuée à chaque élève.
• Description de la figure – mise en évidence de la nécessaire données de deux informations pour décrire une droite précise (2 points de passage ou 1 point de passage et une direction de droites).
• Étude du cas des 5 points alignés permettant d’arriver à une première synthèse du type :
  • « Deux droites perpendiculaires ne peuvent pas être confondues »,
  • « Deux droites parallèles peuvent être confondues ».

Séance 2 : Travail autonome en demi-classe

	Groupe 1	Groupe 2
Première demi-heure	- Construction de la figure sur feuille dans différentes configurations de points (premières constructions en classe de perpendiculaires) - Utilisation d’un exemple de droites perpendiculaires sur calque pour vérifier, par superposition, la construction à l’équerre - Utilisation d’un guide-âne sur transparent pour vérifier approximativement la construction des parallèles tracé dans un premier temps de manière empirique. - Pendant ce temps, l’enseignant peut aider individuellement chaque élève en fonction des difficultés perçues. (Annexe)	Recherche sur Geoplan (figure disponible sur fichier) des configurations possibles avec droites confondues en salle de communication en autonomie [1] avec l’aide-éducateur (Annexe)
Deuxième demi-heure	On inverse les groupes

Séance 3 : Synthèse de la recherche faite en salle informatique

Vidéo-projection de la figure sur Geoplan.

Rappel des données : Cinq points “libres” A, B, C, D et E et quatre droites définies à partir de ces points par : et et Peut-on avoir 2, 3 ou 4 des droites confondues ? Envisager toutes les solutions possibles.

Explicitation orale des cas impossibles en s’appuyant sur la contrainte de perpendicularité des droites et et en argumentant par la phrase copiée lors de la première séance : « Deux droites perpendiculaires ne peuvent pas être confondues ».

Mise en évidence de quelques situations de droites confondues en demandant à quelques élèves de faire la manipulation.

• Explicitation des contraintes nouvelles sur la position des points (hypothèses).
• Premières formulations hypothético-déductives.
• Explicitations de quelques pas de démonstrations qui donnent l’occasion d’expliciter oralement les propriétés sur les directions de droites et en fin de séance de les institutionnaliser.

L’extrait joint de la feuille d’exercices illustre des situations possibles où l’élève pourra réutiliser ces propriétés dans des situations moins magistrales lors des séances suivantes.

Document annexe

format PDF - 19.3 kio

	Si A, D et E sont alignés alors et sont confondues A, D et E alignés donc Or et et donc et sont confondues.
	Si (DE) // (AC) et (AB) (AC) alors et confondues (AC) et [C et donc = (AC) (DE) = // (AC) = et donc et A et A donc sont confondues.

 Fichiers utiles

Fichiers utiles :

La figure dynamique représentant la figure des cinq points et des quatre droites.

Fichier Geoplan format Geoplan-Geospace - 880 octets

Fichier GeoGebra format Fichier GeoGebra - 973 octets

Fichier Cabri-Géométre format Cabri Géométre - 1.6 kio

Remarque :
En fonction de la maîtrise du logiciel par les élèves, on peut éventuellement leur demander de construire cette figure au préalable.

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

• Le dynamisme de la figure permet à la majorité des élèves d’envisager un maximum de situations possibles en peu de temps alors que la recherche avec papier-crayon est plus laborieuse.
  De plus cette situation étant proposée en début d’apprentissage, une maîtrise insuffisante des concepts en jeu (parallèles et perpendiculaires) et de la construction des objets correspondants est un réel obstacle pour la mise en situation de recherche avec papier-crayon.
• La situation permet à l’élève de dépasser la notion de dessin par une première approche de la notion de figure comme ensemble des dessins possibles correspondant à une description donnée.

 Prolongements possibles

On peut par exemple demander : « Les quatre droites peuvent-elles former un rectangle ? ».
L’extrait d’un contrôle commun explicite une possibilité de susciter ce type de recherche auprès de certains élèves.

Document annexe

format PDF - 18.8 kio