Suite arithmétique ou suite géométrique ?

 Présentation de l’activité

Utilisation d’un tableur pour résoudre le problème suivant :

Un jeune technicien supérieur sortant de l’école, qui devra travailler 42 ans, souhaite comparer les salaires proposés par deux entreprises :

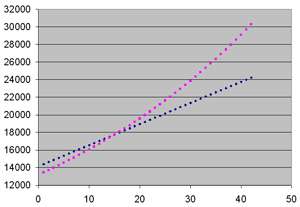
• L’ entreprise B propose un salaire annuel net de 14400 euros avec une augmentation de 240 euros par an.
• L’ entreprise C propose un salaire annuel net de 13440 euros avec une augmentation de 2% par an.

 Public / Niveau

Testé en première STI Sciences et technologies industrielles .

 Objectifs

• Introduction pour le cours sur les suites.

 Durée

• Moins d’une heure en salle informatique suivant le niveau de pratique du tableur.

 Prérequis

• Application d’un pourcentage.

 Déroulement de l’activité

En salle informatique, un élève par poste.

Les élèves vont rapidement remplir les deux colonnes qui permettent de comparer, année par année, les salaires proposés par les deux entreprises.
Le professeur demandera alors un graphique permettant de visualiser les évolutions des deux salaires.
Ensuite il faudra certainement amener les élèves à réfléchir sur la nécessité de calculer la somme des salaires sur les 42 années, dans les deux cas.

Ce travail terminé, le professeur demandera comment on aurait pu faire pour calculer directement et à la main, les salaires de la 10^ième année, puis ceux de la 20^ième année.
Enfin, il faudra établir une formule pour calculer directement les contenus des cellules B_n ou C_n.

Pour les élèves les plus rapides, le professeur pourra demander une conjecture sur des sommes de suites particulières (voir fiche professeur).

Fichiers utiles

La fiche professeur :

Fiche professeur format PDF - 71.7 kio

Fiche professeur format Word - 112 kio

Le fichier tableur :

Fichier tableur format Excel - 20 kio

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

• Introduction naturelle de la notation indicielle des suites, en comparaison avec la dénomination des cellules du tableur.

• Découverte rapide des formules donnant un terme en fonction de son rang et du premier terme de la suite.

• Comparaison rapide d’une suite arithmétique et d’une suite géométrique.

• Calcul rapide des sommes des termes.