Équation du troisième degré avec paramètre
Facile
Manipulation de l’ordinateur
Travail à réaliser à la maison
Présentation de l’activité
Soit ![]() un réel strictement positif.
un réel strictement positif.
Déterminer suivant les valeurs du paramètre ![]() , le nombre de solutions dans l’intervalle [0 ; 2
, le nombre de solutions dans l’intervalle [0 ; 2![]() ], de l’équation :
], de l’équation : ![]() .
.
Ajout du professeur : faire intervenir un support de géométrie dynamique.
Public / Niveau
Terminale S
Durée
Exercice réalisable en une heure à la maison.
Objectifs
Conjecturer suivant les valeurs de ![]() le nombre de solutions de l’équation.
le nombre de solutions de l’équation.
Ce qui a été fait avant
- Étude de fonction.
- Théorème de la bijection (corollaire du théorème des valeurs intermédiaires).
Déroulement de l’activité
Côté des élèves
- Utilisation de GeoGebra :
- pour construire la courbe et un curseur pour faire varier
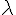 ,
, - pour émettre la conjecture.
- pour construire la courbe et un curseur pour faire varier
- Les élèves ont souvent rendu trois courbes imprimées, chacune représentant les différents résultats obtenus à savoir :
- 0 <
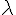 < 1 : pas de solution,
< 1 : pas de solution, -
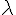 = 1 : une solution,
= 1 : une solution, -
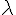 > 1 deux solutions
> 1 deux solutions
- 0 <
- Aucun élève n’a pensé à m’envoyer son fichier par mail ou à l’amener sur une clé. L’impression sur papier leur semblait le seul moyen de rendre quelque chose.
- Démonstration du résultat conjecturé :
- Certains élèves ont dérivé également
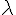 .
. - Peu ont fait une étude correcte.
Beaucoup ont eu des difficultés pour élaborer la discussion. En effet utiliser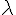 et
et 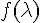 dans le tableau de variation n’est pas “courant” surtout en début d’année.
dans le tableau de variation n’est pas “courant” surtout en début d’année.
- Certains élèves ont dérivé également
Côté du professeur
Utilisation de GeoGebra avec un vidéo-projecteur, pour :
- appuyer la conjecture des élèves à l’aide de la figure.
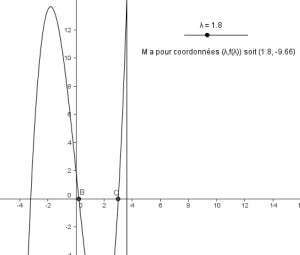
- faire le “parallèle” avec le tableau de variation en utilisant le point M (
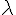 ;
; 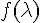 ).
). - insister sur l’importance du tableau de variation dans la discussion avec le théorème de la bijection.
Apport des TICE Technologies de l’information et de la communication pour l’enseignement
Utiliser un curseur pour faire varier ![]() et ainsi pouvoir émettre la conjecture souhaitée.
et ainsi pouvoir émettre la conjecture souhaitée.
Pour information
Personnes à contacter pour cette activité : Guillaume MIANNAY