Le portail

 Présentation de l’activité

Un portail comporte 12 barreaux verticaux, régulièrement espacés.
On veut savoir combien mesure le septième.

 Public / Niveau

Classe de troisième voire classe de quatrième.

 Objectifs

• Partir d’un exercice classique du livre pour aboutir à exploiter les différentes stratégies élèves rencontrées.
• Utilisation de la géométrie dynamique.
• Utilisation du tableur.
• Travail autour de la proportionnalité.

 Ce qui a été fait avant

Rien d’essentiel. L’idée de la propriété de Thalès étant déjà évoquée en classe de quatrième.

 Déroulement de l’activité

Étape 1 : Un travail donné pour le lendemain.
Faire l’exercice suivant dans vos cahiers.

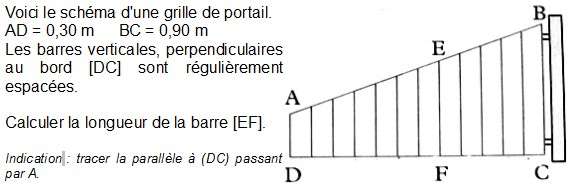
Exercice classique retrouvé dans la plupart des manuels

Les élèves cherchent une solution ou une piste de travail qui peut se résumer en la construction à l’échelle de la figure.

Étape 2 : Retour en classe et analyse des réponses.

On exploite les différentes pistes trouvées.

• Figure à l’échelle
  Elle permet d’avoir une idée de la solution mais n’est pas garante de l’exactitude (toujours ce souci d’imprécision).

• Une longueur arbitraire pour pouvoir utiliser la propriété de Thalès.
  Souvent, comme la longueur entre les barreaux n’est pas données, les élèves en choisissent une arbitrairement pour pouvoir se ramener à une situation de Thalès classique.

• Utilisation de l’algèbre et de la propriété de Thalès.
  Comme la longueur entre les barreaux est indéfinie, on peut poser une lettre pour effectuer les calculs.

• Mise en place d’une stratégie de proportionnalité.
  Au lieu d’imaginer ce problème statiquement, un binôme a eu l’idée de le voir dans le temps, comme une voiture se déplaçant de A vers B en un mouvement uniforme. À chaque barreau, elle a avancé de la même hauteur :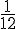 de la différence d’altitude soit 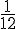de 30 cm.

Étape 3 : Mise en situation dynamique.

Les pistes élèves sont maintenant à exploiter par tous en salle informatique.

Des questions sont en suspend :

• Est ce que si on agrandit la largeur du portail, la hauteur du septième barreau augmente d’autant ?
• A-t-on besoin d’utiliser le théorème de Thalès ?
• Peut-on faire ce travail sans calculs ?

Étape 4 : Tableur et géométrie dynamique.

Un travail en salle informatique permet à chacun d’exploiter numériquement son idée et de se positionner autour d’une idée d’un autre élève vue en classe.

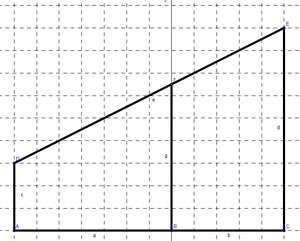
• Utilisation d’un dessin à l’échelle.
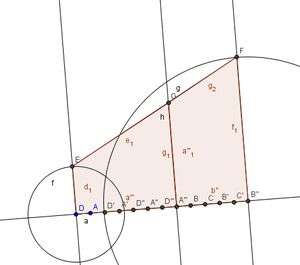
  Sous GeoGebra, une figure utilisant le quadrillage permet rapidement d’avoir la mesure du barreau en question, sans se soucier des contraintes de construction.
  Ici, nous utilisons la géométrie dynamique comme un instrument de mesure plus précis qu’une règle pour la construction et dans la prise de mesure.

Fichier GeoGebra

format Fichier GeoGebra - 1.1 kio

• Utilisation du logiciel de géométrie dynamique pour vérifier.
  Le but est de faire des symétriques pour avoir le même espacement entre les barreaux et ainsi vérifier que les rapports de Thalès sont bien constants. Ici, la théorie et l’expérimentation s’accordent : ouf !

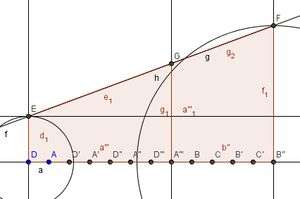
Fichier GeoGebra format Fichier GeoGebra - 2 kio	Fichier GeoGebra Variante format Fichier GeoGebra - 2.2 kio

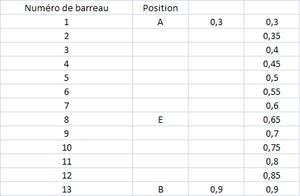
• Utilisation du tableur.
  On avance de case en case en rajoutant un douzième de 30. Ici, un simple travail d’itération permet de conclure.

Fichier tableur

format Excel - 18 kio

 Évaluation

Un travail similaire a été donné en devoir maison avec la possibilité de le rendre de façon numérique.

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

Une ouverture d’esprit.
Ainsi, le prof n’est pas le seul acteur de l’apprentissage de sa classe, chacun peut y poser sa pierre.