Le bon choix

 Présentation de l’activité

Bienvenue dans ce jeu de hasard.
Voici 3 portes.
Une seule contient un trésor et quel trésor ! Une statue en or plus grande que tu ne puisses l’imaginer.

Je te propose d’en choisir une et j’en ouvrirais une qui ne contient rien.
En second lieu, tu auras le choix de garder ta porte ou de l’échanger contre celle qui reste.

 Public / Niveau

• Classe de troisième :
  Idée d’introduction des probabilités en visant deux objectifs en parallèle :
  • Une approche "fréquentiste" de l’idée de probabilité. Pour quelle stratégie, la fréquence nous est favorable ?
  • Une approche théorique en manipulant un arbre de raisonnement.

• Classe de cinquième :
  Idée d’introduction d’une étude statistique facilement manipulable en classe.
  • Le but est de créer un tableau de données statistique pour introduire la notion de fréquence et de classe.

 Objectifs

• Introduire la notion de probabilité par les deux entrées : fréquence et arbre.
• Utiliser le tableur pour offrir une plus grande simulation.

 Ce qui a été fait avant

Rien.

 Déroulement de l’activité

Étape 1 : Utilisation d’une animation HTML permettant de s’imprégner du problème.

• Les élèves manipulent et se positionnent instinctivement pour l’une ou l’autre des possibilités de jeu (stratégie), permettant de pouvoir gagner le plus souvent possible.
• Existe-t-il une stratégie favorable ?

Étape 2 : Analyse des données et interprétation.

Après un travail personnel, on rassemble les données de chacun et on peut conjecturer.

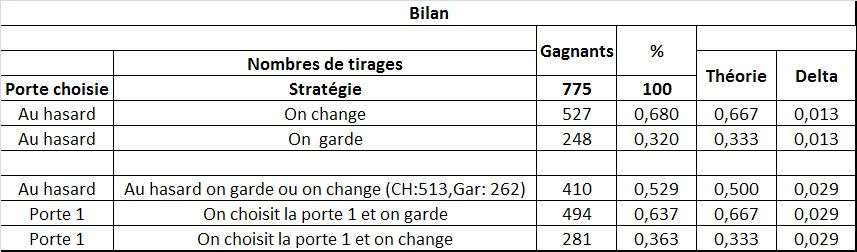
Étape 3 : De la statistique vers les probabilités.

Devons-nous garder ou changer pour avoir une issue favorable ?

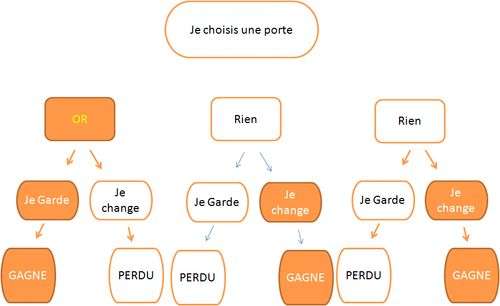
Dans la simulation, nous retrouvons les différents cas possibles.
Notons que si nous n’avons pas de stratégie, il y a 50 % de chances de gagner. Ce qui est apparu lors de la mise en place de cet exercice en classe (moyenne entre et ).

Attention, rien n’est plus aléatoire que le hasard ! Il est possible de perdre avec la stratégie gagnante mais aussi de gagner avec une stratégie quelconque !

 Évaluation

• Un travail ultérieur sur la création de la simulation au tableur est demandé.

 Fichiers utiles

• Le tableau de simulation complet :

Fichier tableur

format Excel - 405 kio

• Une simulation élève :

Fichier tableur élève

format OpenDocument Spreadsheet - 16.8 kio

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

• Une idée d’intégration du sujet et d’envie de trouver son chemin en autonomie.
• C’est la multiplication des stratégies élèves qui permettra de conjecturer en une ouverture probabiliste.