Perpendiculaires et parallèles

 Présentation de l’activité

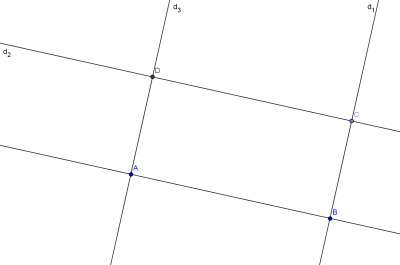
Soient A et B deux points, et soit () la perpendiculaire à la droite (AB) passant par B.
Soit C un point de (). Soient () la parallèle à la droite (AB) passant par C et () la parallèle à la droite () passant par A.
On appelle D le point d’intersection de () et ().
Quelle est la nature du quadrilatère ABCD ?

 Public / Niveau

Sixième

 Ce qui a été fait avant

À l’aide du vidéoprojecteur, le professeur illustre sur GeoGebra les propriétés du cours et en profite pour faire une présentation du logiciel :

• Masquer les axes.
• Utiliser les outils de construction (droite perpendiculaire / droite parallèle).
• Illustrer la différence entre un point libre (créé sans contrainte) et semi-libre (placé sur une droite par exemple).

 Objectifs de la séance

• Découvrir les fonctionnalités d’un logiciel de géométrie dynamique.
• Formuler et démontrer une conjecture.

 Déroulement

• Premier temps : devant le logiciel

Les élèves effectuent la construction sur l’ordinateur.
Le professeur passe dans les rangs pour aider les plus faibles et valide les constructions.
Il invite alors les élèves à « déplacer » les points A, B et C pour qu’ils se rendent compte que le logiciel respecte les contraintes de parallélisme et d’orthogonalité puis pour qu’ils formulent alors une conjecture quant à la nature du quadrilatère ABCD.

• Second temps : sur papier

Les élèves, qui ont accès à leurs cahiers, démontrent cette conjecture à l’aide des propriétés du cours.

 Prolongement possible

Coller une grosse boulette de papier sur la tache.
Construire, en utilisant l’équerre, la droite (T) passant par le point A et perpendiculaire à la droite (d).

 Fichiers utiles

• Énoncé de l’activité :

Énoncé de l’activité format PDF - 211.1 kio

Énoncé de l’activité format Word - 49.5 kio

• Un exemple de fichier GeoGebra :

Fichier GeoGebra

format Fichier GeoGebra - 3.1 kio

• Énoncé du prolongement :

Énoncé du prolongement format PDF - 116.8 kio

Énoncé du prolongement format Word - 118.5 kio