Un problème de construction (le rectangle)
Facile
Utilisation d’un vidéo-projecteur
En classe entière
Présentation de l’activité
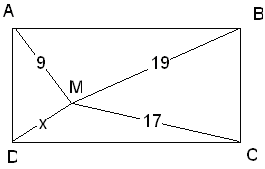
ABCD est un rectangle.
On a mesuré les distances de M à A, B et C.
Construire la figure et déterminer la distance de M à D.
Public / Niveau
- Ce problème a été donné, comme exercice à chercher à la maison, en seconde mais il est certainement possible de le faire en fin de troisième.
- À tester avec d’autres niveaux tels que première S par exemple.
Objectifs
Utiliser un logiciel de géométrie dynamique pour aider les élèves à réaliser une construction sur feuille.
Durée
- Suivant le niveau de la classe, il faut compter presque une heure pour la construction de cette figure, en prenant le temps d’exploiter toutes les notions utilisées.
- On peut compter une autre séance d’une heure en salle informatique pour construire la figure avec un logiciel de géométrie dynamique.
- Il faut encore une séance en classe entière pour traiter la partie théorique.
|
|
|
Pré-requis / Notions investies
- Inégalité triangulaire, intervalles (en seconde).
- Cercles et distances.
- Cercle circonscrit à un triangle rectangle.
- Diagonales du rectangle.
- Symétrie centrale.
- Projection orthogonale.
- Théorème de Pythagore.
- Équations.
Ce qui a été fait avant
- Configurations du plan, équations simples.
- Prise en main d’un logiciel de géométrie dynamique.
Déroulement de l’activité
- Après une première recherche à la maison, les élèves n’ont pas réussi à construire cette figure, ni à déterminer la longueur MD.
- En demi groupe, on décide de construire la figure sur le cahier de l’élève.
Le professeur, grâce au vidéo-projecteur, enverra les images au fur et à mesure, ce qui permet aux élèves de progresser dans la construction, et de débloquer la situation, car les élèves ont peu de chance de réussir la construction sans un peu d’aide.
- Plusieurs solutions pour la construction :
- Les élèves, en général, commencent par construire le rectangle ABCD, mais ils ont peu de chance de réussir.
En effet le problème n’a de solution que si la largeur AD est comprise entre 6 et 12, et cette largeur étant fixée, la longueur AB doit être telle que :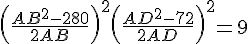 .
.
C’est là qu’un logiciel de géométrie dynamique aura son intérêt par rapport à la figure figée du cahier, puisque, avec l’ordinateur on peut ajuster la largeur et la longueur du rectangle pour que les trois cercles soient sécants en M :
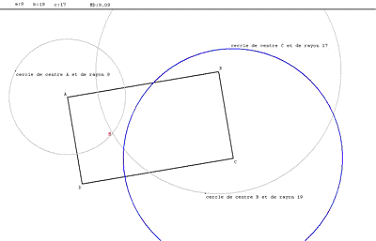
Figure n° 1
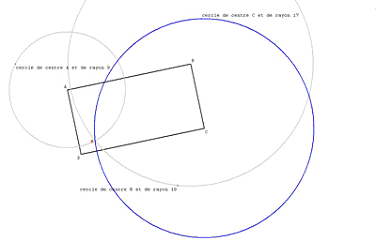
Figure n° 2
Il suffit alors de demander au logiciel d’afficher la longueur cherchée MD. - D’autres élèves, moins nombreux, décident de tracer d’abord le point M.
Pour eux d’autres difficultés se présentent : Les trois cercles de centre M étant construits, il s’agit maintenant d’aller placer un triangle rectangle dont chaque sommet est sur un des cercles précités.
Un élève ayant l’idée d’aller placer son équerre comme il faut, y arrive rapidement, mais cette proposition est peu fréquente, et les autres élèves ont bien du mal à construire ces trois points.
L’image ci-dessous, projetée au tableau, aidera les retardataires à placer les points sur leur cahier.
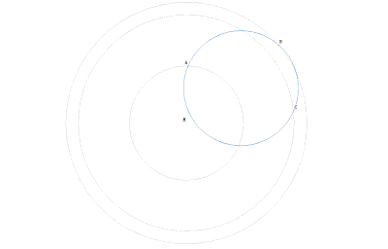
Figure n° 3
Il reste à placer le point D et à lire la distance MD.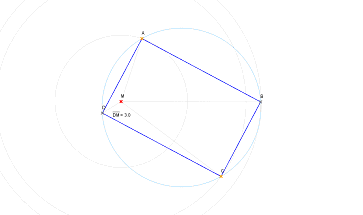
Figure n° 4 - Un autre intérêt du logiciel de géométrie dynamique est de permettre de laisser une trace du lieu d’un point.
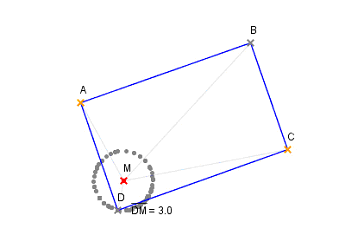
Figure n° 5
- Les élèves, en général, commencent par construire le rectangle ABCD, mais ils ont peu de chance de réussir.
Fichiers utiles
Fichier au format GeoGebra :
- Construction du rectangle ABCD en premier.
Après avoir tracé le rectangle ABCD, de diagonale mobile [AC], on trace les trois cercles de rayons 9, 17 et 19.
Il suffit alors de déplacer les points mobiles A et C de façon à ce que les trois cercles soient sécants en point M.
Il reste à lire la longueur cherchée MD.
- Construction du point M en premier.
Il suffit de déplacer les points mobiles A et C pour trouver la solution.
Fichier au format GeoNext :
- Construction du rectangle ABCD en premier.
Après avoir tracé le rectangle ABCD, de diagonale mobile [AC], on trace les trois cercles de rayons 9, 17 et 19.
Il suffit alors de déplacer les points mobiles A et C de façon à ce que les trois cercles soient sécants en point M.
Il reste à lire la longueur cherchée MD.
-
format GeoNext - 3.4 kio
- Construction du point M en premier.
Il suffit de déplacer les points mobiles A et C pour trouver la solution.
|
|
Fichier au format Geoplan :
- Construction du rectangle ABCD en premier (construction pas à pas).
- Soit d = AC, la longueur de la diagonale. Dans quel intervalle doit varier d pour que le triangle AMC ne soit pas aplatit ?
-
format Geoplan-Geospace - 929 octets
Pour les élèves qui ne connaissent pas l’inégalité triangulaire
En écrivant les trois inégalités triangulaires, on obtient![d \in -]8 ;26[ d \in -]8 ;26[](local/cache-TeX/3e877fa74510f541e021352a20227cf5.png) .
. -
- Pour la construction du point B, on utilise la propriété caractéristique du cercle circonscrit au triangle rectangle de diamètre [AC].
- Construction du point D par symétrie centrale.
- Construction du point M à l’aide de deux cercles.
- Construction du cercle de centre C et de rayon 17.
- Soit d = AC, la longueur de la diagonale. Dans quel intervalle doit varier d pour que le triangle AMC ne soit pas aplatit ?
Reste à déplacer les points A, B, ou C pour amener le point M sur le cercle bleu et à lire en haut et à gauche la valeur de x.
-
format Geoplan-Geospace - 3.7 kio
- Construction du point M en premier.
Il suffit ensuite de placer les points A et C sur les cercles de centre M et de rayons respectifs 9, 17 et 19 puis de tracer le cercle de diamètre [AC].
Une fois la figure terminée, on peut faire : « Sélection Trace Objet D » puis « Mode Trace ».
-
format Geoplan-Geospace - 4.1 kio
Apport des TICE Technologies de l’information et de la communication pour l’enseignement
- La dynamique des figures qui permet aux élèves de visualiser les problèmes de cette construction et finalement de construire la figure sur leur cahier.
- La trace laissée par un objet, ici le point D, et qui permet de conclure en donnant une solution très visuelle.
- L’aspect ludique de la géométrie dynamique.
Prolongements possibles
Liste non exhaustive :
- Dans quel cas le point M est-il à l’intérieur du rectangle ?
- Quand la figure est constructible, quel est le rectangle d’aire maximale ?
Pour information
Personnes à contacter pour cette activité : François GONET & Cyrille DOURIEZ