Le parquet
Activité produite dans le cadre des travaux académiques mutualisés 2012-2013.
Énoncé
Doug n’aime plus le vieux carrelage de son salon et il projette de poser du
parquet pour le cacher.
Il souhaite le poser à l’anglaise.
Sa pièce est rectangulaire et en voici un schéma :
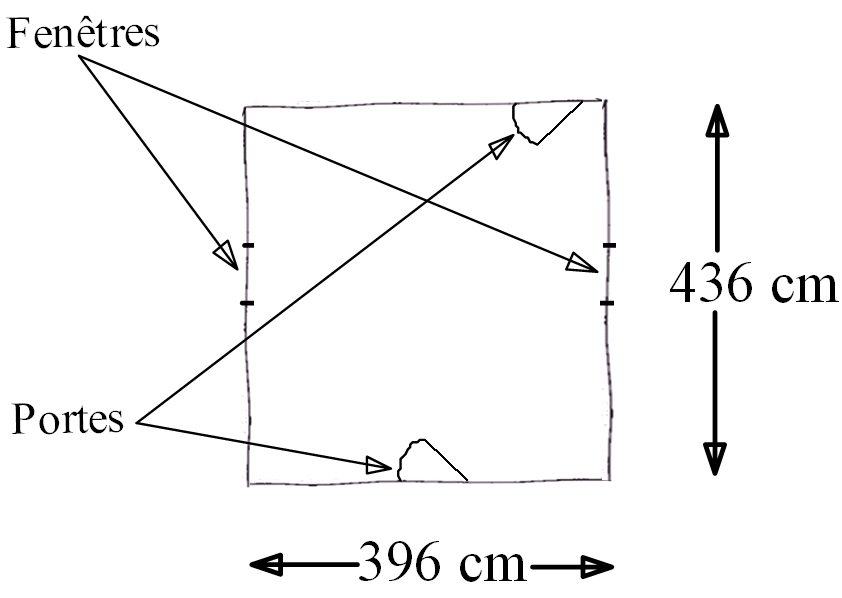
Le parquet qu’il souhaite acheter est vendu par paquet de 8 lames.
Celles-ci sont rectangulaires et mesurent 15 cm sur 120 cm.
Il pense prendre 12 paquets mais il a peur que ce soit un peu juste à cause des découpes.
Voici quelques informations sur la pose qu’il souhaite utiliser :
La pose de parquet à l’anglaise est très répandue.
Ce motif est en effet plus facile à installer et plus économique que d’autres, car il ne génère que très peu de chutes.De plus, elle crée d’agréables lignes de fuite, généralement dirigées vers l’entrée de la lumière.
En pratique, les lames sont installées bout à bout sur une même ligne et une fois arrivé à l’extrémité, on utilise la partie coupée pour la ligne suivante.
Malgré tout, il faut décaler les joints d’une rangée sur l’autre d’au moins 30
cm pour un plus bel aspect final. De plus, il faut laisser un joint de dilatation
de 0,5 cm en périphérie de la pièce.
Votre objectif est d’aider Doug à se rassurer.
Quelles peuvent être les démarches à suivre pour être sûr qu’il aura suffisamment de parquet ?
Niveau
Collège
Présentation
Calcul du nombre de lames pour la pose d’un parquet à l’anglaise dans une
pièce rectangulaire.
Objectifs
- Travailler en groupes sur un problème ouvert (échange d’idées, répartition des tâches, respect des autres).
- Étudier les pratiques des élèves en fonction du matériel dont ils disposent et comparer les différentes démarches (calculatrice, tableur, schéma, calculs à la main).
- Poursuivre l’apprentissage du calcul sous toutes ses formes.
- Utiliser un brouillon pour organiser les idées et faire un compte-rendu de recherche.
Durée
2 heures
Notions réinvesties
- Grandeurs et mesures.
- Sens des opérations.
Place du calcul
- L’activité permet de faire le lien entre soustractions successives et division entière.
- Organisation réfléchie, conception de plusieurs calculs.
- Contrôle des résultats à chaque étape.
- Développer des stratégies à partir d’essais et de tâtonnements à la main ou à la calculatrice, avec un tableur ou un logiciel de géométrie dynamique.
| Organiser | Anticiper | Analyser | Exécuter | Contrôler | Prendre des décisions | Intelligence du calcul | Piloter |
Mise en œuvre
Cette activité a été réalisée avec deux classes de 3ème en début d’année
scolaire.
Des ordinateurs portables étaient à disposition des élèves si besoin.
J’ai demandé une feuille de brouillon par élève et un compte rendu par
groupe.
Sur le compte rendu, j’ai demandé d’écrire toutes les idées qu’ils
avaient eu et d’écrire si elles semblaient « bonnes » ou « mauvaises ».
.J’ai laissé une classe libre sur la démarche et ils se sont mieux organisés pour la recherche.
- ½ h : Travail sur l’énoncé, organisation des groupes
- 1h : Recherche en groupes et compte-rendu du groupe (à l’écrit).
- ½ h : Retour sur les idées de chacun des groupes (par un représentant du groupe) et approfondissement de certaines méthodes.

Apport des Tice Technologies de l’information et de la communication pour l’enseignement
Raisonner et organiser sa démarche pour créer la feuille de calcul pour visualiser plusieurs essais.
Fichiers annexes
- Démarches possibles

|

|
- Copies d’élèves
Aux vues des productions d’élèves, la fonctionnalité « calcul automatisé » semble ne pas avoir été exploitée (ou peu)…
À l’aide d’un schéma et de calculs divers. Un début de raisonnement est présent mais certaines valeurs sont présentées avec peu d’explication.

|

|
- Fichier tableur
|
|
|