Pont sur la seine
Activité produite dans le cadre des travaux académiques mutualisés 2015-2016.
| Groupe Maths et TICE Académie d’Amiens Date de révision de la fiche : janvier 2015 |

|
Présentation de l’activité
À partir d’une photo aérienne issue de Google Maps, les élèves sont invités à réfléchir sur un problème (fictif) de construction de route et de pont.
« Le conseil général de l’Eure souhaite relier les communes de Saint-Pierre-d’Autils (27950) et Pressagny-l’Orgueilleux (27510). Vous êtes chargé d’étudier la solution permettant la construction (route et pont) reliant la D6015 à la D313 la plus courte.
Pour des raisons techniques, la route devra partir de Saint-Pierre d’Autils en suivant le tracé n°1, puis partir en ligne droite vers la Seine, la traverser perpendiculairement, traverser l’Île Chouquet en ligne droite puis l’autre branche de la Seine perpendiculairement et enfin, se terminer en suivant le chemin tracé portant le repère n°2.
On peut considérer qu’à cet endroit, les bords de la Seine ainsi que de l’Île Chouquet sont parallèles. »
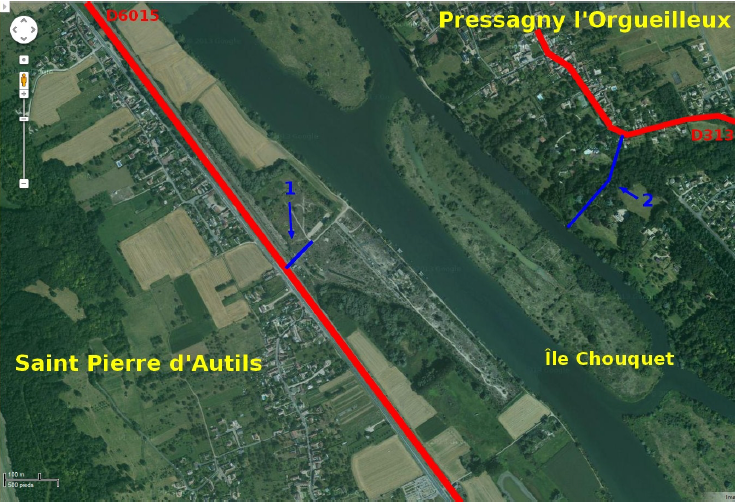
NB : Les élèves disposent de la photo en grande résolution, mise à disposition sur l’ENT Environnement numérique de travail .
Public
Seconde
Première
Séance préalable et prérequis
- Notion de fonction, extremum.
- Utilisation avancée de Géogebra (déjà utilisé à de nombreuses reprises auparavant), comme l’importation de photos, l’utilisation de la seconde fenêtre… Bien qu’on puisse s’en passer...
Objectifs
- Résoudre un problème ouvert concret,
- Modéliser une situation,
- Résoudre un problème d’optimisation,
- Expliquer puis présenter une solution d’un problème,
- Utiliser un outil logiciel pour résoudre le problème,
- Utiliser un outil logiciel pour présenter la solution,
- Choisir le logiciel adéquat pour résoudre un problème.
Déroulement
Ce travail a été donné à deux classes de seconde, avec des modalités différentes : dans l’une, en demi-classe dans une salle disposant de tables « classiques » et d’ordinateurs sur le pourtour ; dans l’autre, en devoir maison.
En classe, les élèves reçoivent l’énoncé papier ainsi que l’adresse de la photo en grande résolution sur l’ENT et sont invités à réfléchir au problème sans aucune aide (aussi bien celle du professeur que d’un outil) pendant 5 à 10 minutes, par groupes de 2 ou 3, afin qu’ils comprennent bien les contraintes du projet. La façon de construire les ponts perpendiculaires aux berges n’est pas évidente pour tous immédiatement !
Une fois les contraintes bien cernées, les élèves dans leur grande majorité tentent des constructions « papier », mesurent, conjecturent… Puis l’idée de l’utilisation de l’outil informatique fait jour chez la plupart d’entre eux, sans pour autant que l’utilisation de géogebra soit naturelle.
Mais dès que les groupes les plus avancés montrent quelque chose à l’écran, toute la classe « se rallie » à l’utilisation de ce logiciel.
La modélisation sous géogebra est difficile. Ils arrivent à faire apparaître la position
optimale du pont, sans mettre cela en lien avec une fonction. Mais alors se pose la question :
- « Comment transmettre cette information aux équipes d’ouvriers chargés de la construction ?
- Comment peut-on leur transmettre de façon précise la position du pont ? »
L’idée naît alors qu’il faut indiquer la position du pont par une distance à un point fixe… Et la sonnerie retentit.
Une seconde heure de travail sera nécessaire pour finir le travail et pour présenter une solution du problème.
Prolongement
La position du pont serai-elle la même si la route 1 se poursuivant (en ligne droite) jusqu’à la Seine et que la route 2 s’arrêtait à son « coude » ?
Liens utiles
-
format Fichier GeoGebra - 250.3 kio