Trouver le puits

Auteur : Francois Delannoy

 Présentation de l’activité

 Public

Cycle 4

 Séances préalables

• Notion de médiatrice
• Cercle circonscrit d’un triangle
• Notion d’équidistance

 Objectifs

Comprendre de manière ludique et dynamique les propriétés du centre du cercle circonscrit à un triangle.

 Déroulement

• L’élève ouvre le fichier Geogebra trouver_le_puits.ggb :

Fichier GeoGebra

format Fichier GeoGebra - 1.5 Mio

Il lit la consigne. (puis clique sur CONSIGNE pour accéder à la situation)

Une première approche :

• Tentative de résolution par essais/erreurs.
• Une fois résolu, l’enseignant actionne le curseur « coup de vent ». Le puits n’est alors plus au bon endroit.

Réflexion sur une stratégie à adopter :

• Détermination d’une stratégie pour placer le puits à équidistance des trois maisons.
  (On pourra commencer par déterminer les positions du puits équidistantes de deux maisons)

Retour à l’oral, mise en commun des idées :

• Retour sur la méthode à employer.
• Les élèves effectuent ensuite les constructions pour placer le puits.
  Attention : Pour cela, les élèves ne disposent pas de tous les outils de Geogebra.

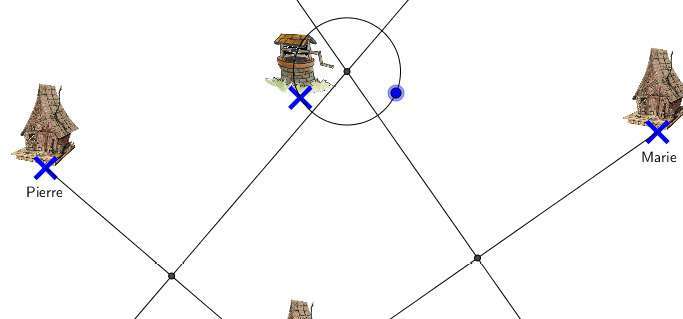
Astuce pour placer le puits :

• Tracer les médiatrices, placer leur point de concours.
• Construire un cercle (Centre-Point) de centre ce point d’intersection
• Lier le point matérialisant le puits à ce cercle.
• Réduire le rayon du cercle.

 Fichiers utiles :

Fiche scénario

format PDF - 284.1 kio

Fichier GeoGebra

format Fichier GeoGebra - 1.5 Mio