AP Autonomie : du statut du faux

Date de révision de la fiche : décembre 2016
Auteur : Jean-Philippe BLAISE

 Étape 1 : Visionnage de la vidéo suivante :

Résolution d’une équation du second degré à l’aide d’un couvercle de Nutella

Questionnement :

• Est-ce possible ?
• Pouvons-nous le tester ?
• Quelle est la précision de solutions proposées ?
• Est-ce transposable à d’autres équations ?
• Pourquoi ne l’avoir jamais appris en classe ?

 Étape 2 : Partie critique

A l’aide du document Geogebra disponible, vérifions cette construction.

Pot de Nutella

format Fichier GeoGebra - 13.2 kio

Questionnement :

• Que pouvons-nous en conclure ?
• Pourrions-nous refaire la construction nous-même ?

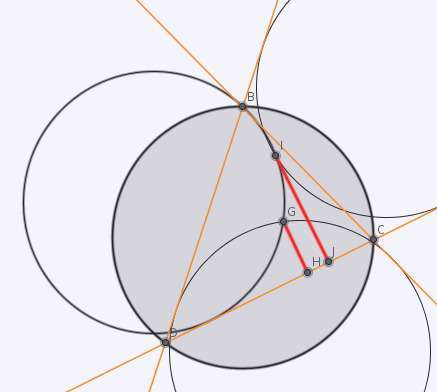
 Étape 3 : Partie mathématique

Questionnement :

• Quelle est la taille d’un couvercle de pot de Nutella ?
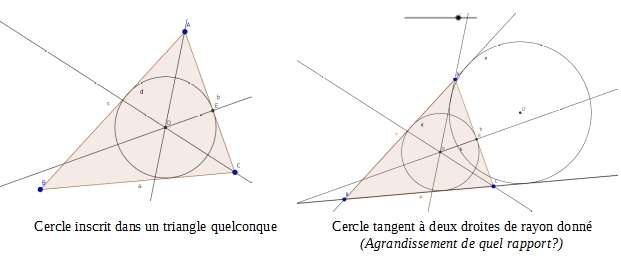
• Comment construire le triangle de départ sous géogébra ?
• Comment construire un cercle inscrit dans un triangle particulier ?
• Comment construire un cercle tangent à deux droites dont on connaît le rayon ?

 Fiche

AP Autonomie : du statut du faux

format PDF - 652.2 kio