Puissance d’un point par rapport à un cercle

 Présentation de l’activité

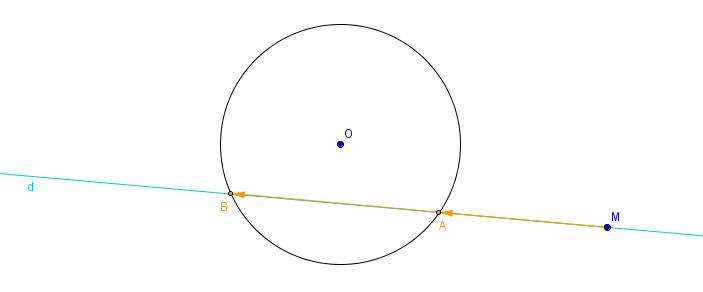
(C) est un cercle, M un point du plan et d une droite passant par M. On se propose d’étudier le produit scalaire où A et B sont les points d’intersection, lorsqu’ils existent, de la droite d et du cercle (C).

 Public / Niveau

Testé en première S mais également réalisable en classe de première STI Sciences et technologies industrielles

 Objectifs

• Utiliser un logiciel de géométrie dynamique pour émettre des conjectures
• Réinvestir les connaissances sur le produit scalaire pour démontrer ces conjectures en s’aidant des apports visuels et dynamiques du logiciel.

 Durée

• Une séance d’une heure en salle informatique pour faire la construction, émettre les conjectures puis faire les démonstrations.
• Une demi-heure pour la correction et prolonger la question.

 Notions réinvesties

• Relation de Chasles.
• Identité remarquable.
• Propriétés opératoires du produit scalaire.

 Ce qui a été fait avant

Utilisation du projeté orthogonal pour le calcul d’un produit scalaire

 Déroulement de l’activité

• [20 min] : Lecture de l’énoncé (pas de grand problème rencontré) et recherche des propriétés du produit scalaire étudié, mise en commun des conjectures.
• [10 min] : Début de la démonstration : construction d’un point auxiliaire (le point diamétralement opposé à A) puis utilisation du projeté orthogonal.
• [15 min] : Démonstration de la propriété d’invariance du produit scalaire.
• [10 min] : Démonstration du signe du produit scalaire.

 Évaluation

Il y aura évaluation à 3 niveaux :

• Réalisation de la figure
• Émission des conjectures à partir de la figure dynamique
• Rédaction des démonstrations

 Fichiers utiles

• Le fichier d’appropriation du problème :

(C) est un cercle, M un point du plan et d une droite passant par M.
On se propose d’étudier le produit scalaire où A et B sont les points d’intersection, lorsqu’ils existent, de la droite d et du cercle (C).
Bouger, soit le point vert pour déplacer la droite d, soit le point M. 

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

• La version finale

Figure GeoGebra - Version finale

format HTML - 917 octets

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

• Utilisation d’un logiciel de géométrie dynamique GeoGebra pour faire apparaître une figure facilement exploitable.
• Le dynamisme de la figure est primordial à l’élève pour émettre les conjectures.
• Les données analytiques du logiciel permettent de contrôler à chaque étape de la démonstration, ses résultats.

 Prolongements possibles

On peut par exemple chercher le lieu des points M dont on connaît la puissance par rapport au cercle (introduction aux lignes de niveau).

Dans le document suivant, on cherche l’ensemble des points M dont la puissance par rapport au cercle (C) est égale à 20.
Pour cela, il suffit de bouger le point M.
Si M est en bleu, la puissance de M par rapport à (C) est strictement supérieure à 20 et si M est en vert, la puissance de M par rapport à (C) est strictement inférieure à 20.

Figure GeoGebra - Prolongement

format HTML - 923 octets