Indice de masse corporelle

 Présentation de l’activité

C’est un problème ouvert :
Il y a deux méthodes pour établir une relation entre la masse et la taille d’un individu adulte de corpulence normale :

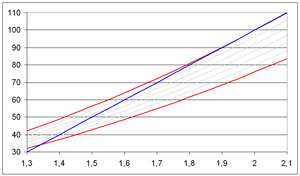
• Une première possibilité consiste à faire le calcul suivant : Taille 1,50 m donc 50 kg … Taille 1,80 m donc 80 kg … De même pour une taille quelconque.
• Une deuxième possibilité consiste à utiliser l’indice de masse corporelle (IMC [1])

On demande aux élèves de comparer ces deux méthodes. On s’intéresse aux individus de taille comprise entre 1,30 m et 2,10 m.

 Public / Niveau

Testé en première STI Sciences et technologies industrielles , utilisable en seconde.

 Objectifs

L’objectif principal est d’apprendre aux élèves à modéliser le problème donné.
Dans un premier temps, l’utilisation d’un tableur permet de reconnaître, dans la première méthode, une fonction affine, et dans la deuxième méthode, une fonction du second degré.
Dans un deuxième temps, l’utilisation de GeoGebra oblige les élèves à mettre en œuvre les formules mathématiques adéquates, et à les utiliser, ce qui est notre objectif principal.

 Pré-requis

Bonne connaissance du tableur et de GeoGebra.

 Ce qui a été fait avant

Généralités sur les fonctions, fonctions de référence, fonctions affines en seconde, second degré et dérivation en première.

 Déroulement de l’activité

• En classe entière :
  Le professeur expose le problème ouvert et laisse le débat s’installer, éventuellement il oriente vers l’outil informatique.
• Séance en salle informatique, en demi groupe :
  Il est souhaitable de proposer d’abord une étude sur le tableur, puis de passer sur Geogebra afin de modéliser le problème.
  Deux heures au moins sont nécessaires suivant l’habileté des élèves.
• Un petit temps de réflexion à la maison, et une séance en classe entière avec le vidéo-projecteur pour la synthèse, et l’étude des prolongements.
  On pourra aussi exploiter les graphiques avec des questions du type : « Une personne considérée en surcharge pondérale avec la première méthode est-elle aussi en surcharge pondérale avec la 2ème ? ».

Fichier tableur format Excel - 34 kio

Fichier GeoGebra format Fichier GeoGebra - 1.1 kio

 Fichiers utiles

Les fichiers élèves très détaillés pour les classes faibles :

Fichier élève format PDF - 64.8 kio

Fichier élève format Word - 106 kio

 Prolongements possibles

• Les élèves peuvent proposer une troisième relation du type fonction affine entre la masse et la taille d’un individu de corpulence normale, qui serait plus en concordance avec l’IMC.

Fichier GeoGebra

format Fichier GeoGebra - 1 kio

• En première, on peut faire étudier les points d’intersection entre la fonction affine de la première méthode, et l’enveloppe proposée par la deuxième méthode (IMC ).
  On pourra aussi constater et démontrer que la droite représentant la fonction affine de la première méthode, n’est autre que la tangente au point d’abscisse 2, à la courbe représentative de la fonction correspondant à un IMC de 25 ! Coïncidence ?

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

Ce problème ouvert n’est pas facilement gérable en seconde ou en première sans un tableur.

Le grapheur oblige l’élève à modéliser le problème, les curseurs de GeoGebra permettent facilement de proposer une troisième relation du type fonction affine.