Trinôme du second degré

 Présentation de l’activité

• Utilisation d’une feuille de calcul permettant de calculer le discriminant et les éventuelles racines d’un trinôme du second degré, puis la somme S et le produit P de ces racines

• Utilisation d’une deuxième feuille de calcul permettant de construire un tableau de valeurs et la parabole représentative du trinôme.

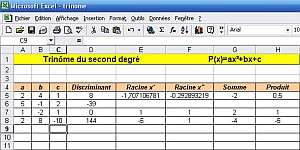
 Public / Niveau

Testé en première STI Sciences et technologies industrielles , utilisable en première S et ES.

 Objectifs

• Comprendre le rôle des coefficients a, b, c, par rapport au discriminant et aux racines éventuelles du trinôme du second degré.
• Établir une conjecture sur le lien entre la somme S, le produit P et ces coefficients a, b, c.

 Durée

• Une heure en salle informatique en demi groupe pour la création et l’utilisation des feuilles de calcul.

• Une heure en classe entière avec le vidéo-projecteur pour la synthèse, la démonstration des formules de S et P, et les applications.

 Pré-requis

Racines d’un polynôme, tableau de valeurs, courbe représentative.

 Ce qui a été fait avant

Début du cours sur le second degré : le discriminant et les éventuelles racines.

 Déroulement de l’activité

Première séance en salle informatique :

Le professeur distribue la fiche élève, et laisse une demi-heure pour la création des deux feuilles de calcul.
Il aide les élèves les moins rapide. Pour ceux qui n’ont pas terminé, on peut distribuer le fichier tout fait.

Il doit rester 25 minutes aux élèves pour remplir les cellules, faire les différents essais, et pour imprimer chacune des deux feuilles de calculs ainsi remplies.

Deuxième séance en classe entière :

Avec le vidéo-projecteur, on revient sur la première feuille de calcul pour établir une conjecture entre la somme S, le produit P et les coefficients a, b, c.
Une fois établie, la démonstration est faite au tableau.

Il reste à voir les applications.
Le professeur pourra finaliser en utilisant ce fichier GeoGebra, dans lequel on peut faire varier les coefficients à l’aide de curseurs :

S’il vous plaît, installer Java 1.5 (ou ultérieur) pour visualiser cette page.

 Fichiers utiles

• Trois versions sont proposées suivant le niveau de connaissance du tableur :

Version “clefs en main” pour les débutants	Version pour les initiés	Version pour les experts
Fiche élève format PDF - 46.7 kio Fiche élève format Word - 97 kio	Fiche élève format PDF - 46.9 kio Fiche élève format Word - 95.5 kio	Fiche élève format PDF - 52.9 kio Fiche élève format Word - 123 kio
Fichier tableur format Excel - 26 kio	Fichier tableur format Excel - 20 kio

• La fiche professeur :

Fiche professeur format PDF - 93.7 kio

Fiche professeur format Word - 203.5 kio

 Apport des TICE Technologies de l’information et de la communication pour l’enseignement

Outre l’aspect ludique, très apprécié, cette activité permet aux élèves, même les plus faibles, d’établir rapidement la conjecture demandée et de voir concrètement l’effet des coefficients sur la parabole.

Par ailleurs, la relation entre une cellule du tableur et son contenu, est la même qu’entre la lettre représentant le coefficient et sa valeur, ce qui aide bien pour la compréhension des formules en général.

 Prolongements possibles

On peut utiliser cette activité pour visualiser graphiquement le signe du trinôme suivant les valeurs de la variable x, dans les différents cas de signe du discriminant.

Pour des élèves scientifiques, on peut se poser de nombreuses autres questions, comme par exemple : Si les coefficients sont des nombres premiers, le trinôme peut il avoir une et une seule racine ?